题目内容
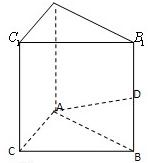
P是平面ABCD外的点，四边形ABCD是平行四边形，
=（2，-1，-4），
=（4，2，0），
=（-1，2，-1）．
（1）求证：PA⊥平面ABCD；
（2）对于向量
=（x1，y1z1），
=(x2y2z2)，
=(x3y3z3)，定义一种运算：(
×
)•
=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2z3-x3y2z1，试计算(
×
)-
的绝对值；说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算(
×
)-
的绝对值的几何意义．
| AB |
| AD |
| AP |
（1）求证：PA⊥平面ABCD；
（2）对于向量
| a |
| b |
| c |
| a |
| b |
| c |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |
（1）
•
=(2，-1，-4)•(-1，2，-1)=-2+(-2)+4=0，∴
⊥
，即AP⊥AB．
•
=(-1，2，-1)•(4，2，0)=-4+4+0=0，即PA⊥AD．
∴PA⊥面ABCD．
（2）|(
×
)•
|=48，又cos?
•
＞=
，
V=
|
|•|
|•sin?
•
＞•|
|=16
猜测：|(
×
)•
|在几何上可表示以AB，AD，AP为棱的平行六面体的体积（或以AB，AD，AP为棱的四棱柱的体积）．
| AP |
| AB |
| AP |
| AB |
| AP |
| AD |
∴PA⊥面ABCD．
（2）|(
| AB |
| AD |
| AP |
| AB |
| AD |
| 3 | ||
|
V=
| 1 |
| 3 |
| AB |
| AD |
| AB |
| AD |
| AP |
猜测：|(
| AB |
| AD |
| AP |
练习册系列答案
阅读快车系列答案
相关题目
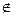平面ABC，PA=PB=PC，∠APB=∠APC=60°，∠BPC=90°求证：平面ABC⊥平面PBC
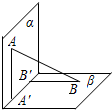
a∥b;②a∥c,b∥c