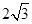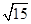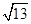题目内容
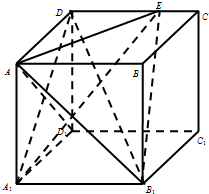
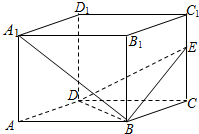
在长方体ABCD-A1B1C1D1中,AA1=AD=2,点E在棱CD上,且CE=
CD.
(1)求证:AD1⊥平面A1B1D;
(2)在棱AA1上是否存在点P,使DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由;
(3)若二面角A-B1E-A1的余弦值为
,求棱AB的长.
| 1 |
| 3 |
(1)求证:AD1⊥平面A1B1D;
(2)在棱AA1上是否存在点P,使DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由;
(3)若二面角A-B1E-A1的余弦值为
| ||
| 6 |

(1)证明:在长方体ABCD-A1B1C1D1中,∵A1B1⊥面A1D1DA,
∴A1B1⊥AD1.
在矩形A1D1DA中,∵AA1=AD=2,
∴AD1⊥A1D.
又A1D∩A1B1=A1,
∴AD1⊥平面A1B1D.
(2)如图,在长方体ABCD-A1B1C1D1中,以D1为原点建立空间直角坐标系D1-xyz.
依题意可知,D1(0,0,0),A1(2,0,0),D(0,0,2),A(2,0,2),
设AB的长为x,则C1(0,x,0),B1(2,x,0),C(0,x,2),E(0,
x,2).
假设在棱AA1上存在点P,使得DP∥平面B1AE.
设点P(2,0,y),则
=(2,0,y-2),
=(0,0,y-2).
易知
=(-2,-
x,2),
=(-2,
x,0).
设平面B1AE的一个法向量为n=(a,b,c),
则
,即
.
令b=3得,a=x,c=
x,∴
=(x,3,
x).
∵DP∥平面B1AE,∴
•
=0且DP?平面B1AE.
得2x+(y-2)•
x=0,∴y=
.
∴
=(0,0,-
),|
|=
,
∴AP的长为
.
(3)∵CD∥A1B1,且点E∈CD,
∴平面A1B1E、平面A1B1D与面A1B1CD是同一个平面.
由(1)可知,AD1⊥面A1B1D,
∴
=(2,0,2)是平面A1B1E的一个法向量.
由(2)可知,平面B1AE的一个法向量为n=(x,3,
x).
∵二面角A-B1E-A1的余弦值为
,
∴cosθ=
=
=
,解得x=3
.
故AB的长为3
.

∴A1B1⊥AD1.
在矩形A1D1DA中,∵AA1=AD=2,
∴AD1⊥A1D.
又A1D∩A1B1=A1,
∴AD1⊥平面A1B1D.
(2)如图,在长方体ABCD-A1B1C1D1中,以D1为原点建立空间直角坐标系D1-xyz.
依题意可知,D1(0,0,0),A1(2,0,0),D(0,0,2),A(2,0,2),
设AB的长为x,则C1(0,x,0),B1(2,x,0),C(0,x,2),E(0,
| 2 |
| 3 |
假设在棱AA1上存在点P,使得DP∥平面B1AE.
设点P(2,0,y),则
| DP |
| AP |
易知
| B1E |
| 1 |
| 3 |
| AE |
| 2 |
| 3 |
设平面B1AE的一个法向量为n=(a,b,c),
则
|
|
令b=3得,a=x,c=
| 3 |
| 2 |
| n |
| 3 |
| 2 |
∵DP∥平面B1AE,∴
| DP |
| n |
得2x+(y-2)•
| 3 |
| 2 |
| 2 |
| 3 |
∴
| AP |
| 4 |
| 3 |
| AP |
| 4 |
| 3 |
∴AP的长为
| 4 |
| 3 |
(3)∵CD∥A1B1,且点E∈CD,
∴平面A1B1E、平面A1B1D与面A1B1CD是同一个平面.
由(1)可知,AD1⊥面A1B1D,
∴
| D1A |
由(2)可知,平面B1AE的一个法向量为n=(x,3,
| 3 |
| 2 |
∵二面角A-B1E-A1的余弦值为
| ||
| 6 |
∴cosθ=
| ||
| 6 |
|
| ||||
|
|
| |2x+3x| | ||||||
2
|
| 2 |
故AB的长为3
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
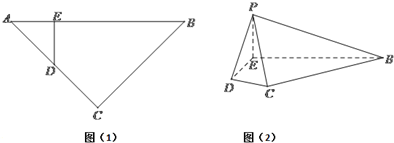
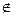 平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC
平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC
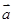 和
和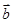 的夹角为1200,
的夹角为1200,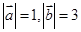 ,则
,则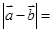 ( ).
( ).