题目内容
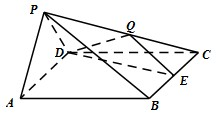
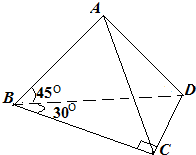
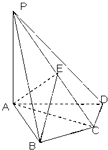
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)证明:CD⊥AE;
(2)证明:PD⊥平面ABE;
(3)求二面角B-PC-D的余弦值.
(1)证明:CD⊥AE;
(2)证明:PD⊥平面ABE;
(3)求二面角B-PC-D的余弦值.

证明:(1)PA⊥底面ABCD,
∴CD⊥PA.
又CD⊥AC,PA∩AC=A,
∴CD⊥面PAC,AE?面PAC,
∴CD⊥AE.
(2)PA=AB=BC,∠ABC=60°,
∴PA=AC,E是PC的中点,
∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,
∴AE⊥PD.易知BA⊥PD,
∴PD⊥面ABE.
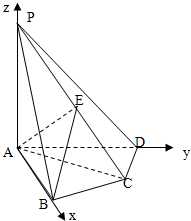
(3)由题可知PA,AB,AD两两垂直,如图建立空间直角坐标系,
设AB=2,则B(2,0,0),C(1,
,0),P(0,0,2),D(0,
,0)
设平面PBC的一个法向量为
=(x,y,z),
=(2,0,-2),
=(-1,
,0)
,即
,
取y=
,则x=z=3
即
=(3,
,3)
设面PDC的一个法向量为
=(x,y,z),
=(1,
,-2),
=(0,
,-2)
,即
取y=
,则x=1,z=2,
即
=(1,
,2)
∴cos<
,
>=
=
=
由图可知钝二面角B-PC-D的余弦值为-
.(12分)
∴CD⊥PA.
又CD⊥AC,PA∩AC=A,
∴CD⊥面PAC,AE?面PAC,
∴CD⊥AE.
(2)PA=AB=BC,∠ABC=60°,
∴PA=AC,E是PC的中点,
∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,
∴AE⊥PD.易知BA⊥PD,
∴PD⊥面ABE.
(3)由题可知PA,AB,AD两两垂直,如图建立空间直角坐标系,
设AB=2,则B(2,0,0),C(1,
| 3 |
| 4 | ||
|
设平面PBC的一个法向量为
| m |
| PB |
| BC |
| 3 |
|
|
取y=
| 3 |
即
| m |
| 3 |
设面PDC的一个法向量为
| n |
| PC |
| 3 |
| PD |
| 4 | ||
|
|
|
取y=
| 3 |
即
| n |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| 3+3+6 | ||||
|
| ||
| 7 |
由图可知钝二面角B-PC-D的余弦值为-
| ||
| 7 |


练习册系列答案
相关题目