题目内容
【题目】椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的两个动点,若直线
上的两个动点,若直线![]() 的斜率乘积为定值
的斜率乘积为定值![]() ,则动直线
,则动直线![]() 恒过定点的坐标为__________.
恒过定点的坐标为__________.
【答案】![]()
【解析】当直线BC的斜率存在时,设直线BC的方程为y=kx+m,
由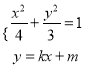 ,消去y得:(3+4k2)x2+8kmx+4m2﹣12=0,
,消去y得:(3+4k2)x2+8kmx+4m2﹣12=0,
设B(x1,y1),C(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又A(﹣2,0),由题知kABkAC=![]() =﹣
=﹣![]() ,
,
则(x1+2)(x2+2)+4y1y2=0,且x1,x2≠﹣2,
则x1x2+2(x1+x2)+4+4(kx1+m)(kx2+m)
=(1+4k2)x1x2+(2+4km)(x1+x2)+4m2+4
=![]() +(2+4km)
+(2+4km)![]() +4m2+4=0
+4m2+4=0
则m2﹣km﹣2k2=0,
∴(m﹣2k)(m+k)=0,
∴m=2k或m=﹣k.
当m=2k时,直线BC的方程为y=kx+2k=k(x+2).
此时直线BC过定点(﹣2,0),显然不适合题意.
当m=﹣k时,直线BC的方程为y=kx﹣k=k(x﹣1),此时直线BC过定点(1,0).
当直线BC的斜率不存在时,若直线BC过定点(1,0),B、C点的坐标分别为(1, ![]() ),(1,﹣
),(1,﹣![]() ),满足kABkAC=﹣
),满足kABkAC=﹣![]() .
.
综上,直线BC过定点(1,0).
故答案为:(1,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目