题目内容
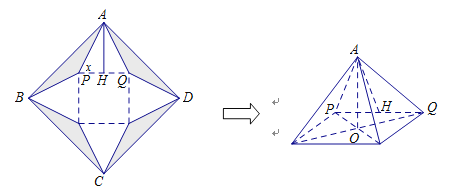
【题目】如图:设一正方形纸片ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中![]() ,O为正四棱锥底面中心.
,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
【答案】(1)![]() 立方分米(2)
立方分米(2)![]() 平方分米
平方分米
【解析】试题分析: (I)若正四棱锥的棱长都相等,则在正方形ABCD中,三角形APQ为等边三角形,由此先计算出此正四棱锥的棱长,再利用正棱锥的性质计算其体积即可;
(II)先利用等腰三角形APQ的底角为x的特点,将侧棱长和底边长分别表示为x的函数,再利用棱锥的体积计算公式将棱锥体积表示为关于x的函数,最后可利用均值定理求函数的值域
试题解析:
(Ⅰ)设正四棱锥底面边长为y分米,由条件知△APQ为等边三角形,
又![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴ .
.
由![]() ,即
,即![]() 得
得![]() .
.
∴
![]() .
.
答:这个正四棱锥的体积是![]() 立方分米
立方分米
(Ⅱ)设正四棱锥底面边长为y,则![]() .
.
由![]() ,即
,即![]() 得
得![]() .
.
∴![]() 即为所求表达式.
即为所求表达式.
∵![]() ,∴
,∴![]() ,
,
令![]() ,则
,则![]() ,
,
由 对
对![]() 恒成立知函数在
恒成立知函数在![]() 上为减函数.
上为减函数.
(或者分子、分母同时除以![]() ,利用“对勾函数”进行说明)
,利用“对勾函数”进行说明)
∴![]() 平方分米即为所求侧面积的范围.
平方分米即为所求侧面积的范围.

练习册系列答案
相关题目

