题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() (
(![]() ),且
),且![]() .
.
(1)证明![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,且
,且![]() 证明
证明![]() ;
;
(3)在(2)小问的条件下,若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】分析:(1)根据题设条件,利用等比数列的定义,即可判定数列![]() 是等比数列,进而求解数列
是等比数列,进而求解数列![]() 的通项公式;
的通项公式;
(2)由(1),得![]() ,进而得到
,进而得到![]() ,即可利用放缩法,证得
,即可利用放缩法,证得![]() ;
;
(3)当![]() 恒成立时,即
恒成立时,即![]() 恒成立
恒成立
设![]() ,分类讨论求得函数
,分类讨论求得函数![]() 的最大值,即可求得实数
的最大值,即可求得实数![]() 的取值范围.
的取值范围.
详解:(1)在![]() 中
中
令![]() ,得
,得![]() 即
即![]() ,
,
∵ ![]() 解得
解得![]()
当![]() 时,由
时,由![]()
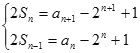 ,得到
,得到![]()
则![]()
又![]() ,则
,则![]()
![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
![]() ,即
,即![]()
![]() ,则
,则![]() ,
,
当![]() 时
时![]() ,
,
当![]() 时,
时,![]() ,
,

综上,![]()
(3)当![]() 恒成立时,即
恒成立时,即![]() (
(![]() )恒成立
)恒成立
设![]() (
(![]() ),
),
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 满足条件;
满足条件;
当![]() 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当![]() 时,由于对称轴
时,由于对称轴![]()
![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
![]() 恒成立,则
恒成立,则![]() 满足条件,
满足条件,
综上所述,实数λ的取值范围是![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了了解某城市居民用水量的情况,我们获得100位居民某年的月均用水量(单位:吨)通过对数据的处理,我们获得了该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏)
100位居民月均用水量的频率分布表
组号 | 分组 | 频数 | 频率 |
1 |
| 4 | 0.04 |
2 |
| 0.08 | |
3 |
| 15 | |
4 |
| 22 | |
5 |
|
| |
6 |
| 14 | 0.14 |
7 |
| 6 |
|
8 |
| 4 | 0.04 |
9 |
| 0.02 | |
合 计 | 100 | ||

(1)确定表中![]() 与
与![]() 的值;
的值;
(2)求频率分布直方图中左数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图;
(4)我们想得到总体密度曲线,请回答我们应该怎么做?

