Question

【题目】已知函数，且．

(1)判断函数的奇偶性；

(2) 判断函数在(1，＋∞)上的单调性，并用定义证明你的结论；

(3)若，求实数a的取值范围．

Answer 1

【答案】（1）f(x)为奇函数；（2）见解析；（3）(0,1)∪(1，＋∞).

【解析】本题考查函数的性质，考查学生的计算能力，证明函数的单调性按照取值、作差、变形定号，下结论的步骤进行．

（1）函数为奇函数．确定函数的定义域，利用奇函数的定义，即可得到结论；

（2）按照取值、作差、变形定号，下结论的步骤进行证明，作差后要因式分解．

（3）根据函数单调性，得到不等式的解集。

解 ∵，且

∴，解得

(1) 为奇函数，

证：∵，定义域为，关于原点对称…

又

所以为奇函数

（2）在上的单调递增

证明：设，

则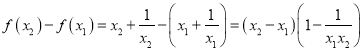

∵

∴ ，

故 ，即， 在上的单调递增

又，即，所以可知

又由的对称性可知时， 同样成立 ∴