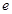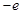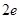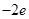题目内容
已知函数f(x)=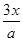 -2
-2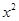 +lnx.
+lnx.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在区间[1,2]上为单调递增函数,求实数a的取值范围.
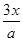 -2
-2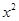 +lnx.
+lnx.(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在区间[1,2]上为单调递增函数,求实数a的取值范围.
(Ⅰ)见解析 (Ⅱ)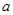 的取值范围是
的取值范围是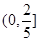 .
.
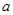 的取值范围是
的取值范围是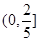 .
. (1)当a=1时,解析式确定,可利用导数等于零,求出极值。但要注意定义域。
(II)本小题转化为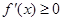 在[1,2]上恒成立,即
在[1,2]上恒成立,即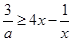 在
在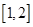 恒成立,再转化为函数最值问题求解。
恒成立,再转化为函数最值问题求解。
(Ⅰ)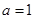 时,
时,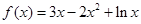 ,定义域为
,定义域为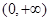 . …………1分
. …………1分
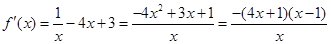
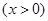 ,………3分
,………3分
当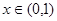 ,
,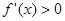 ,函数
,函数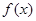 单调递增;
单调递增;
当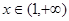 ,
,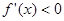 ,函数
,函数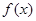 单调递减,…………………5分
单调递减,…………………5分
∴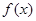 有极大值
有极大值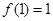 ,无极小值.………………………………6分
,无极小值.………………………………6分
(Ⅱ)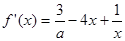 ,……7分
,……7分
∵ 函数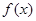 在区间
在区间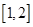 上为单调递增函数,∴
上为单调递增函数,∴ 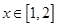 时,
时,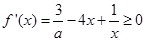 恒成立.即
恒成立.即 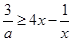 在
在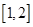 恒成立,…………9分
恒成立,…………9分
令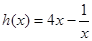 ,因函数
,因函数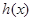 在
在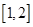 上单调递增,所以
上单调递增,所以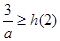 ,即
,即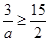 ,…11分
,…11分
解得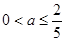 ,即
,即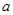 的取值范围是
的取值范围是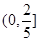 .
.
(II)本小题转化为
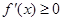 在[1,2]上恒成立,即
在[1,2]上恒成立,即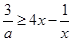 在
在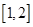 恒成立,再转化为函数最值问题求解。
恒成立,再转化为函数最值问题求解。(Ⅰ)
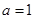 时,
时,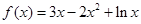 ,定义域为
,定义域为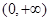 . …………1分
. …………1分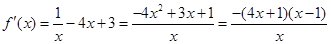
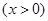 ,………3分
,………3分当
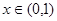 ,
,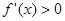 ,函数
,函数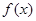 单调递增;
单调递增;当
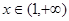 ,
,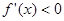 ,函数
,函数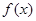 单调递减,…………………5分
单调递减,…………………5分∴
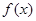 有极大值
有极大值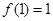 ,无极小值.………………………………6分
,无极小值.………………………………6分(Ⅱ)
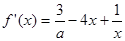 ,……7分
,……7分∵ 函数
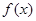 在区间
在区间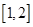 上为单调递增函数,∴
上为单调递增函数,∴ 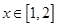 时,
时,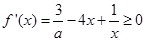 恒成立.即
恒成立.即 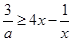 在
在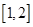 恒成立,…………9分
恒成立,…………9分令
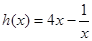 ,因函数
,因函数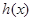 在
在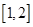 上单调递增,所以
上单调递增,所以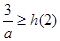 ,即
,即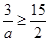 ,…11分
,…11分解得
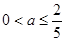 ,即
,即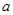 的取值范围是
的取值范围是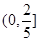 .
.
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
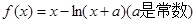 .
.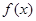 的单调区间;
的单调区间;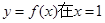 处取得极值时,若关于
处取得极值时,若关于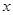 的方程
的方程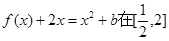 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数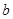 的取值范围;
的取值范围;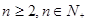 时,有
时,有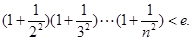
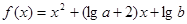 满足
满足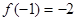 且对于任意
且对于任意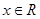 , 恒有
, 恒有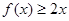 成立
成立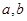 的值; (2)解不等式
的值; (2)解不等式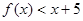
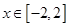 时,函数
时,函数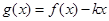 是单调函数,求实数
是单调函数,求实数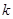 的取值范围。
的取值范围。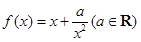 在区间
在区间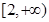 上单调递增,那么实数
上单调递增,那么实数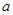 的取值范围是( )
的取值范围是( )
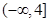


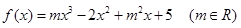 且
且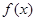 在
在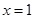 处取得极小值
处取得极小值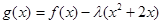 在
在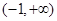 上是增函数,求实数
上是增函数,求实数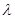 的取值范围。
的取值范围。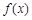 是定义在
是定义在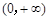 上的非负可导函数,且满足
上的非负可导函数,且满足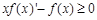 ,对任意正数m,n若
,对任意正数m,n若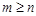 ,则
,则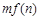 与
与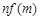 的大小关系是
的大小关系是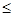 ,
,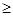 ,或=)
,或=)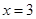 是函数
是函数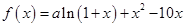 的一个极值点.
的一个极值点.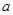 ;
;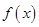 的单调区间;
的单调区间;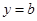 与函数
与函数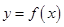 的图象有3个交点,求
的图象有3个交点,求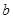 的取值范围.
的取值范围.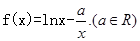
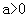 ,试判断函数
,试判断函数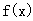 在定义域内的单调性;
在定义域内的单调性;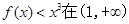 上恒成立,求实数
上恒成立,求实数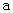 的取值范围。
的取值范围。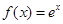 ,则
,则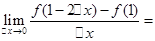 ( )
( )