题目内容
已知函数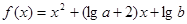 满足
满足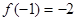 且对于任意
且对于任意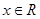 , 恒有
, 恒有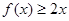 成立
成立
(1)求实数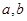 的值; (2)解不等式
的值; (2)解不等式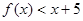
(3)当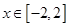 时,函数
时,函数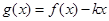 是单调函数,求实数
是单调函数,求实数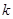 的取值范围。
的取值范围。
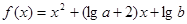 满足
满足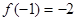 且对于任意
且对于任意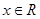 , 恒有
, 恒有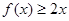 成立
成立(1)求实数
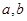 的值; (2)解不等式
的值; (2)解不等式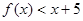
(3)当
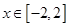 时,函数
时,函数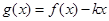 是单调函数,求实数
是单调函数,求实数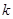 的取值范围。
的取值范围。(1)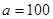 (2)
(2)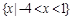 (3)
(3)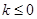 或
或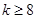
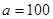 (2)
(2)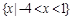 (3)
(3)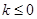 或
或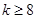
本试题主要是考查了函数的单调性的运用,以及对数运算性质,和不等式的求解的综合运用试题。
(1)利用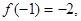 ,得到关于a,b的对数函数关系式,以及
,得到关于a,b的对数函数关系式,以及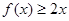 不等式恒成立,借助于二次函数的性质,得到判别式小于等于零,解得
不等式恒成立,借助于二次函数的性质,得到判别式小于等于零,解得
(2)根据已知函数解析式,那么得到关于x的一元二次不等式的求解。
(3)中,因为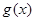 在
在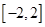 是单调函数,结合二次函数的性质可知,结论
是单调函数,结合二次函数的性质可知,结论
(1) 由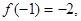 知,
知, 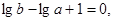 …① ∴
…① ∴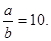 …②------2分
…②------2分
又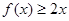 恒成立, 有
恒成立, 有 恒成立,故
恒成立,故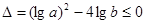 .
.
将①式代入上式得: , 即
, 即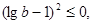 故
故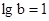 .
.
即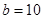 , 代入② 得,
, 代入② 得,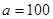 ----- -------6分
----- -------6分
(2)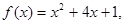
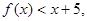 即
即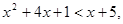 ∴
∴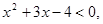
解得: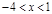 , ∴不等式的解集为
, ∴不等式的解集为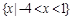 ------9分
------9分
(3)∵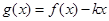 ∴
∴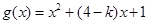
∵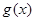 在
在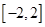 是单调函数
是单调函数
∴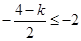 或
或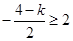 -----------------11分
-----------------11分
解得: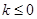 或
或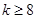
(1)利用
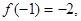 ,得到关于a,b的对数函数关系式,以及
,得到关于a,b的对数函数关系式,以及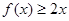 不等式恒成立,借助于二次函数的性质,得到判别式小于等于零,解得
不等式恒成立,借助于二次函数的性质,得到判别式小于等于零,解得(2)根据已知函数解析式,那么得到关于x的一元二次不等式的求解。
(3)中,因为
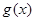 在
在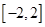 是单调函数,结合二次函数的性质可知,结论
是单调函数,结合二次函数的性质可知,结论(1) 由
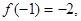 知,
知, 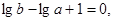 …① ∴
…① ∴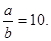 …②------2分
…②------2分又
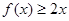 恒成立, 有
恒成立, 有 恒成立,故
恒成立,故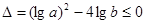 .
.将①式代入上式得:
 , 即
, 即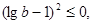 故
故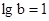 .
.即
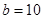 , 代入② 得,
, 代入② 得,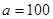 ----- -------6分
----- -------6分(2)
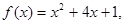
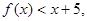 即
即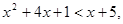 ∴
∴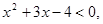
解得:
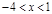 , ∴不等式的解集为
, ∴不等式的解集为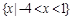 ------9分
------9分(3)∵
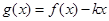 ∴
∴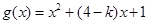
∵
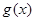 在
在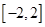 是单调函数
是单调函数 ∴
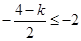 或
或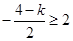 -----------------11分
-----------------11分解得:
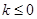 或
或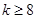

练习册系列答案
相关题目
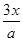 -2
-2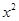 +lnx.
+lnx.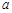 为实数,
为实数,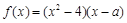 ,
,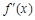 为
为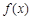 的导函数.
的导函数.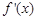 ;
;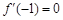 ,求
,求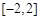 上的最大值和最小值;
上的最大值和最小值;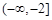 和
和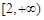 上都是递增的,求
上都是递增的,求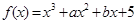 ,过曲线
,过曲线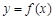 上的点
上的点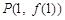 的切线斜率为3.
的切线斜率为3.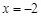 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;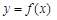 在
在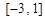 上最大值;
上最大值;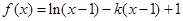
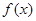 的单调区间;
的单调区间;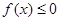 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;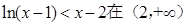 上恒成立
上恒成立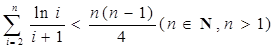
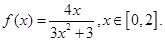
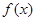 的值域;
的值域;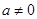 ,函数
,函数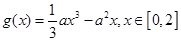 .若对任意
.若对任意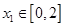 ,总存在
,总存在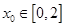 ,使
,使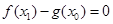 ,求实数
,求实数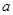 的取值范围.
的取值范围.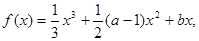 (
(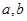 为常数)在
为常数)在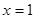 和
和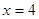 处取得极值,
处取得极值,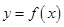 的解析式;
的解析式;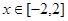 时,
时,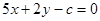 的下方,求实数
的下方,求实数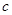 的取值范围.
的取值范围.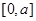 上的函数
上的函数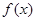 的图象如右下图所示,记以
的图象如右下图所示,记以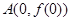 ,
,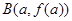 ,
,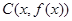 为顶点的三角形的面积为
为顶点的三角形的面积为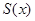 ,则函数
,则函数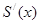 的图象大致是
的图象大致是