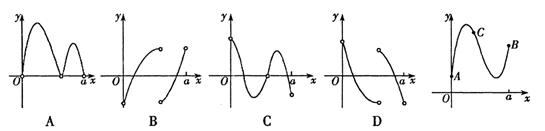
题目内容
已知函数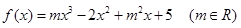 且
且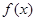 在
在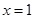 处取得极小值
处取得极小值
(1)求m的值。
(2)若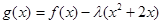 在
在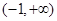 上是增函数,求实数
上是增函数,求实数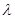 的取值范围。
的取值范围。
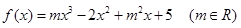 且
且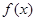 在
在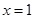 处取得极小值
处取得极小值(1)求m的值。
(2)若
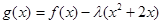 在
在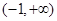 上是增函数,求实数
上是增函数,求实数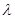 的取值范围。
的取值范围。(1)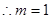 (2)
(2)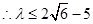
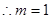 (2)
(2)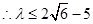
(1)对函数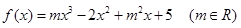 求导,当
求导,当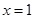 时,令导函数为0,求出
时,令导函数为0,求出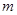 的值,要代入到原函数中进行验证,保证在
的值,要代入到原函数中进行验证,保证在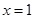 处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数
处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数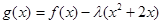 在
在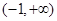 上是增函数,就是
上是增函数,就是
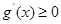 在
在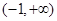 上恒成立,把
上恒成立,把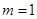 代入分离参数整理得
代入分离参数整理得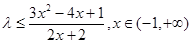 恒成立,只需
恒成立,只需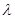 小于等于右边的最小值,利用不等式求出
小于等于右边的最小值,利用不等式求出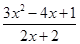 在
在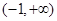 上的最小值,即得
上的最小值,即得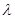 的范围。
的范围。
(1)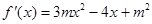
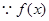 在
在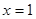 处取得极小值
处取得极小值
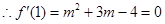 得
得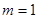 或
或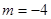
当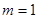 时
时 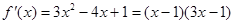
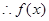 在
在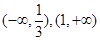 上是增函数在
上是增函数在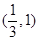 上是减函数
上是减函数
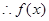 在
在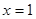 处取得极小值
处取得极小值
当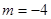 时
时 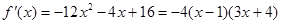
在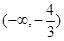
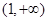 上是减函数 在
上是减函数 在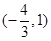 上是增函数
上是增函数
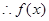 在
在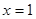 处取得极大值极大值 ,不符题意
处取得极大值极大值 ,不符题意
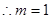 (6分)
(6分)
(2)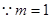
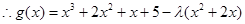
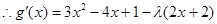
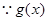 在
在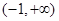 上是增函数,
上是增函数,
 不等式
不等式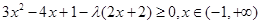
恒成立即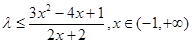 恒成立
恒成立
令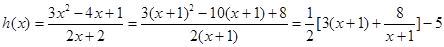
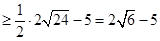 当
当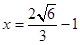 时等号成立
时等号成立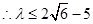
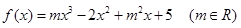 求导,当
求导,当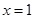 时,令导函数为0,求出
时,令导函数为0,求出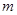 的值,要代入到原函数中进行验证,保证在
的值,要代入到原函数中进行验证,保证在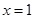 处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数
处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数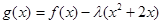 在
在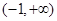 上是增函数,就是
上是增函数,就是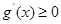 在
在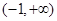 上恒成立,把
上恒成立,把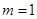 代入分离参数整理得
代入分离参数整理得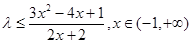 恒成立,只需
恒成立,只需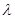 小于等于右边的最小值,利用不等式求出
小于等于右边的最小值,利用不等式求出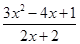 在
在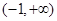 上的最小值,即得
上的最小值,即得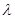 的范围。
的范围。(1)
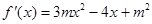
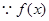 在
在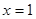 处取得极小值
处取得极小值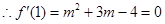 得
得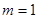 或
或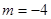
当
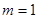 时
时 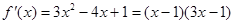
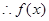 在
在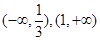 上是增函数在
上是增函数在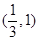 上是减函数
上是减函数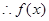 在
在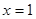 处取得极小值
处取得极小值当
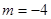 时
时 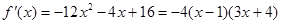
在
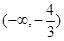
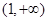 上是减函数 在
上是减函数 在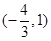 上是增函数
上是增函数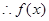 在
在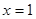 处取得极大值极大值 ,不符题意
处取得极大值极大值 ,不符题意 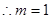 (6分)
(6分)(2)
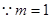
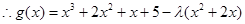
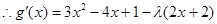
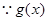 在
在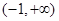 上是增函数,
上是增函数, 不等式
不等式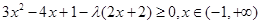
恒成立即
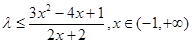 恒成立
恒成立令
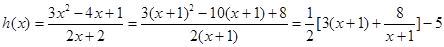
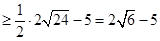 当
当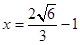 时等号成立
时等号成立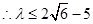

练习册系列答案
相关题目
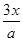 -2
-2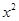 +lnx.
+lnx.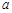 为实数,
为实数,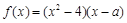 ,
,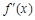 为
为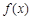 的导函数.
的导函数.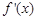 ;
;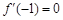 ,求
,求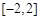 上的最大值和最小值;
上的最大值和最小值;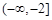 和
和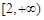 上都是递增的,求
上都是递增的,求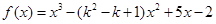 ,
,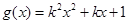 ,其中
,其中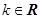 .
. 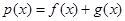 ,若
,若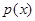 在区间
在区间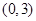 是单调函数,求
是单调函数,求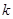 的取值范围;
的取值范围;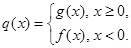 ,是否存在
,是否存在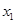 ,存在惟一的非零实数
,存在惟一的非零实数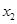 (
(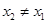 ),使得
),使得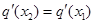 成立?若存在,求
成立?若存在,求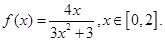
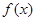 的值域;
的值域;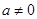 ,函数
,函数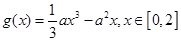 .若对任意
.若对任意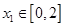 ,总存在
,总存在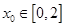 ,使
,使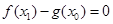 ,求实数
,求实数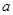 的取值范围.
的取值范围.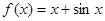
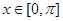 时,求
时,求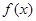 的值域
的值域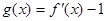 ,若
,若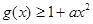 在
在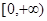 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围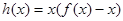 ,若
,若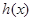 在
在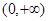 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列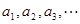 ,
,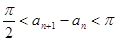
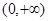 上为增函数的是 ( )
上为增函数的是 ( )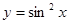
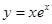
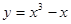
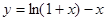
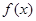 ,设其导函数
,设其导函数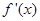 ,当
,当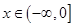 时,恒有
时,恒有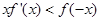 ,令
,令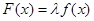 ,则满足
,则满足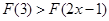 的实数x的取值范围是( )
的实数x的取值范围是( )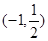
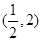
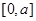 上的函数
上的函数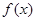 的图象如右下图所示,记以
的图象如右下图所示,记以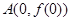 ,
,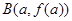 ,
,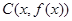 为顶点的三角形的面积为
为顶点的三角形的面积为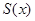 ,则函数
,则函数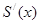 的图象大致是
的图象大致是