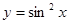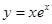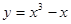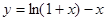题目内容
(本小题满分14分)已知函数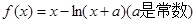 .
.
(1)求函数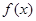 的单调区间;
的单调区间;
(2)当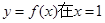 处取得极值时,若关于
处取得极值时,若关于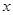 的方程
的方程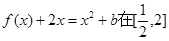 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数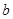 的取值范围;
的取值范围;
(3)求证:当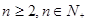 时,有
时,有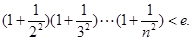
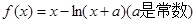 .
.(1)求函数
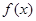 的单调区间;
的单调区间;(2)当
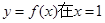 处取得极值时,若关于
处取得极值时,若关于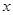 的方程
的方程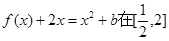 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数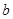 的取值范围;
的取值范围;(3)求证:当
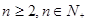 时,有
时,有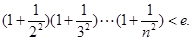
(1)增区间: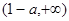 ,减区间:
,减区间: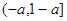 ; (2)
; (2)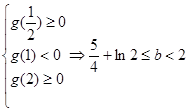
(3)见解析。
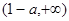 ,减区间:
,减区间: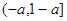 ; (2)
; (2)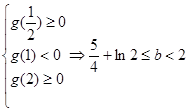
(3)见解析。
本试题主要是考查了导数在研究函数中的运用,求解函数的单调区间和极值问题以及运用导数证明不等式的问题的综合运用。
(1)分析定义域,然后求导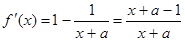 ,然后对于导数大于零或者小于零作出讨论,得到单调区间。
,然后对于导数大于零或者小于零作出讨论,得到单调区间。
(2)因为当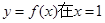 处取得极值时,若关于
处取得极值时,若关于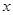 的方程
的方程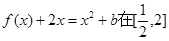 上恰有两个不相等的实数根,结合函数图像来得到不等式。
上恰有两个不相等的实数根,结合函数图像来得到不等式。
(3)由(1)、(2)可得,当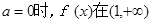 为增函数
为增函数
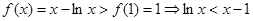 ,然后放缩法得到证明。
,然后放缩法得到证明。
(1)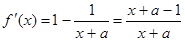
增区间: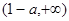 减区间:
减区间: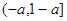 ……………………3分
……………………3分
(2)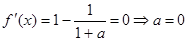
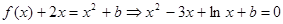
令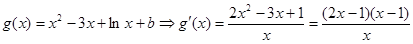
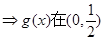 为增函数,
为增函数,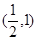 为减函数,
为减函数,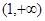 为增函数……………………5分
为增函数……………………5分
则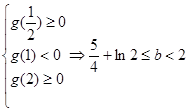 …………………………………………………7分
…………………………………………………7分
(3)由(1)、(2)可得,当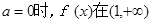 为增函数
为增函数
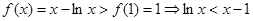 …………………………………………10分
…………………………………………10分
令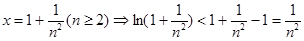 ………………………………12分
………………………………12分
则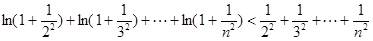
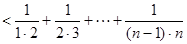 ………………13分
………………13分
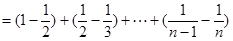
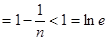
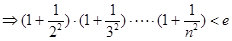 ………………………………………………14分
………………………………………………14分
(1)分析定义域,然后求导
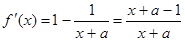 ,然后对于导数大于零或者小于零作出讨论,得到单调区间。
,然后对于导数大于零或者小于零作出讨论,得到单调区间。(2)因为当
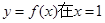 处取得极值时,若关于
处取得极值时,若关于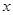 的方程
的方程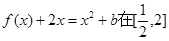 上恰有两个不相等的实数根,结合函数图像来得到不等式。
上恰有两个不相等的实数根,结合函数图像来得到不等式。(3)由(1)、(2)可得,当
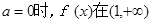 为增函数
为增函数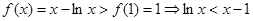 ,然后放缩法得到证明。
,然后放缩法得到证明。(1)
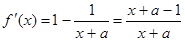
增区间:
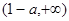 减区间:
减区间: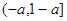 ……………………3分
……………………3分(2)
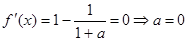
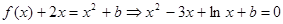
令
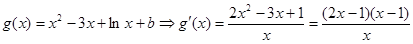
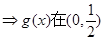 为增函数,
为增函数,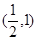 为减函数,
为减函数,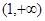 为增函数……………………5分
为增函数……………………5分则
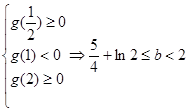 …………………………………………………7分
…………………………………………………7分(3)由(1)、(2)可得,当
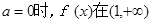 为增函数
为增函数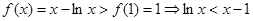 …………………………………………10分
…………………………………………10分令
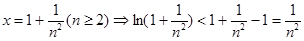 ………………………………12分
………………………………12分则
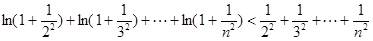
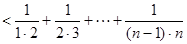 ………………13分
………………13分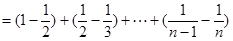
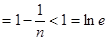
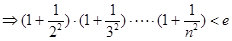 ………………………………………………14分
………………………………………………14分
练习册系列答案
相关题目
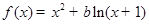 .
.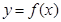 在定义域上是单调函数,求
在定义域上是单调函数,求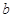 的取值范围;
的取值范围;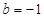 ,证明对于任意的
,证明对于任意的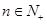 ,不等式
,不等式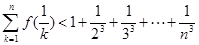 .
.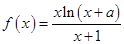
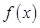 在
在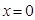 处取到极值,求
处取到极值,求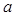 的值.
的值.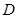 上的函数
上的函数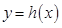 在点
在点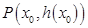 处的切线方程为
处的切线方程为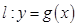 ,若
,若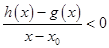 在
在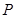 为函数的
为函数的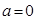 时,试问函数
时,试问函数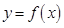 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.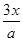 -2
-2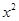 +lnx.
+lnx.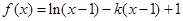
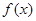 的单调区间;
的单调区间;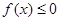 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;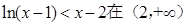 上恒成立
上恒成立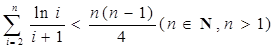
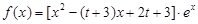 ,
,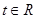
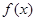 在
在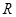 上无极值,求
上无极值,求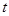 值;
值;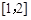 上的最小值
上的最小值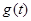 表达式;
表达式;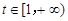 ,任意的
,任意的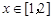 ,均有
,均有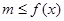 成立,求
成立,求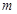 的取值范围.
的取值范围.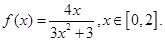
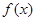 的值域;
的值域;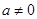 ,函数
,函数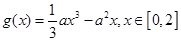 .若对任意
.若对任意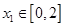 ,总存在
,总存在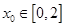 ,使
,使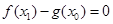 ,求实数
,求实数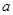 的取值范围.
的取值范围.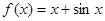
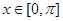 时,求
时,求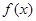 的值域
的值域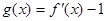 ,若
,若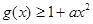 在
在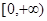 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围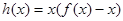 ,若
,若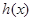 在
在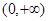 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列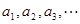 ,
,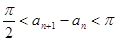
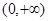 上为增函数的是 ( )
上为增函数的是 ( )