题目内容
【题目】已知椭圆![]() 的左、右焦点为别为F1、F2,且过点
的左、右焦点为别为F1、F2,且过点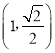 和
和 .
.

(1)求椭圆的标准方程;
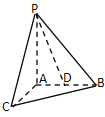
(2)如图,点A为椭圆上一位于x轴上方的动点,AF2的延长线与椭圆交于点B,AO的延长线与椭圆交于点C,求△ABC面积的最大值,并写出取到最大值时直线BC的方程.
【答案】(1)![]() (2)y=
(2)y=![]()
【解析】
(1)将两点代入椭圆方程,求出a,b,然后求解椭圆的标准方程.
(2)设AF2的方程为x=ty+1,联立直线与椭圆方程,利用韦达定理以及弦长公式,点到直线的距离求解三角形的面积结合基本不等式求解最值,然后求解BC的方程即可.
解:(1)将两点代入椭圆方程,有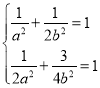 解得
解得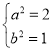 ,
,
所以椭圆的标准方程为![]() .
.
(2)因为A在x轴上方,可知AF2斜率不为0,故可以设AF2的方程为x=ty+1,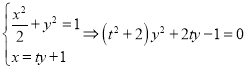 ,
,
得 ,所以
,所以![]() ,
,
设原点到直线AF2的距离为d,则![]() ,
,
所以S△ABC=2S△OAB
=![]()
=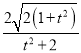
=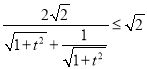 ,△ABC面积的最大值为
,△ABC面积的最大值为![]() .
.
在t=0时取到等号成立,此时AB的方程为:x=1,
可得,A(1,![]() ),B(1,-
),B(1,-![]() ),C(-1,
),C(-1,![]() ),
),
此时BC的方程为:y=![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目