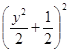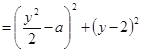题目内容
【题目】已知点![]() 是直线
是直线![]() 上一动点,PA、PB是圆
上一动点,PA、PB是圆![]() 的两条切线,A、B为切点,若四边形PACB面积的最小值是2,则
的两条切线,A、B为切点,若四边形PACB面积的最小值是2,则![]() 的值是
的值是
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】C
【解析】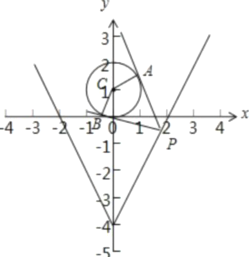
![]() 圆的方程为
圆的方程为![]() 圆心
圆心![]() ,半径
,半径![]() ,根据题意,若四边形面积最小,当圆心与点
,根据题意,若四边形面积最小,当圆心与点![]() 的距离最小时,即距离为圆心到直线
的距离最小时,即距离为圆心到直线![]() 的距离最小时,切线长
的距离最小时,切线长![]() 最小,切线长为
最小,切线长为![]() ,
, ![]() ,
, ![]() 圆心到直线
圆心到直线![]() 的距离为
的距离为![]() ,直线方程为
,直线方程为![]() ,即
,即![]() ,解得
,解得![]() 所求直线的斜率为
所求直线的斜率为![]() ,故选C.
,故选C.
【方法点晴】本题主要圆的方程与性质以及圆与直线的位置关系,属于难题. 解决解析几何中的最值问题一般有两种方法:一是几何意义,特别是用曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法.

练习册系列答案
相关题目