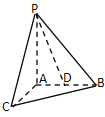
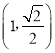题目内容
【题目】如图,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点
的中点
(1)求![]() 与
与![]() 所成角的大小
所成角的大小
(2)求![]() 与平面
与平面![]() 所成的角的大小
所成的角的大小
(3)求![]() 绕直线
绕直线![]() 旋转一周所构成的旋转体的体积
旋转一周所构成的旋转体的体积
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)取![]() 中点
中点![]() ,由平行关系知所求角为
,由平行关系知所求角为![]() ;在
;在![]() 中求得
中求得![]() ,利用勾股定理可求得
,利用勾股定理可求得![]() 三边长,由余弦定理得到
三边长,由余弦定理得到![]() ,进而得到结果;
,进而得到结果;
(2)由线面垂直的判定方法可证得![]() 平面
平面![]() ,由线面角定义知所求角为
,由线面角定义知所求角为![]() ,在
,在![]() 中由长度关系得到
中由长度关系得到![]() ,进而求得结果;
,进而求得结果;
(3)由旋转特点可知得到的旋转体为一个大圆锥挖去一个小圆锥,结合圆锥体积公式可求得结果.
(1)取![]() 中点
中点![]() ,连接
,连接![]()
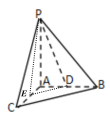
![]() 分别为
分别为![]() 中点
中点 ![]()
![]() 异面直线
异面直线![]() 与
与![]() 所成角即为
所成角即为![]() 与
与![]() 所成角,即
所成角,即![]()
又![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
即异面直线![]() 与
与![]() 所成角为
所成角为![]()
(2)![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
又![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 即为
即为![]() 与平面
与平面![]() 所成角
所成角
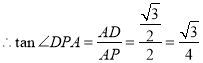
![]()
即![]() 与平面
与平面![]() 所成角为
所成角为![]()
(3)由题意知,所得旋转体是以![]() 为底面半径,
为底面半径,![]() 为高的圆锥中挖去一个以
为高的圆锥中挖去一个以![]() 为底面半径,
为底面半径,![]() 为高的小圆锥
为高的小圆锥
![]() 所得旋转体体积
所得旋转体体积![]()

练习册系列答案
相关题目
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有![]() 多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的
多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的![]() 件工艺品测得重量(单位:
件工艺品测得重量(单位:![]() )数据如下表:
)数据如下表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合计 |
|
(1)求出频率分布表中实数![]() ,
,![]() 的值;
的值;
(2)若从仿制的![]() 件工艺品重量范围在
件工艺品重量范围在![]() 的工艺品中随机抽选
的工艺品中随机抽选![]() 件,求被抽选
件,求被抽选![]() 件工艺品重量均在范围
件工艺品重量均在范围![]() 中的概率.
中的概率.