题目内容
已知 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
.

(Ⅰ)求 外接圆的方程;
外接圆的方程;
(Ⅱ)一动圆过点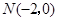 ,且与
,且与 的外接圆外切,求此动圆圆心的轨迹
的外接圆外切,求此动圆圆心的轨迹 的方程;
的方程;
(Ⅲ)过点 斜率为
斜率为 的直线与曲线
的直线与曲线 交于相异的
交于相异的 两点,满足
两点,满足 ,求
,求 的取值范围.
的取值范围.
 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
(Ⅰ)求
 外接圆的方程;
外接圆的方程;(Ⅱ)一动圆过点
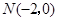 ,且与
,且与 的外接圆外切,求此动圆圆心的轨迹
的外接圆外切,求此动圆圆心的轨迹 的方程;
的方程;(Ⅲ)过点
 斜率为
斜率为 的直线与曲线
的直线与曲线 交于相异的
交于相异的 两点,满足
两点,满足 ,求
,求 的取值范围.
的取值范围.(Ⅰ)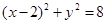 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)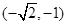
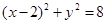 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)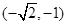
试题分析:(Ⅰ)

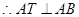 ,从而直线AC的斜率为
,从而直线AC的斜率为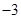 .
.所以AC边所在直线的方程为
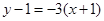 .即
.即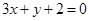 .
. 由
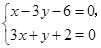 得点
得点 的坐标为
的坐标为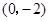 ,
,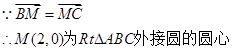
又
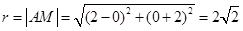 .
. 所以
 外接圆的方程为:
外接圆的方程为: 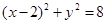 .
. (Ⅱ)设动圆圆心为
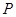 ,因为动圆过点
,因为动圆过点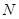 ,且与
,且与 外接圆
外接圆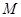 外切,
外切,所以
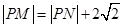 ,即
,即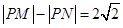 .
. 故点
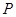 的轨迹是以
的轨迹是以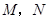 为焦点,实轴长为
为焦点,实轴长为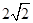 ,半焦距
,半焦距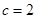 的双曲线的左支.
的双曲线的左支. 从而动圆圆心的轨迹方程
 为
为 .
.(Ⅲ)
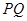 直线方程为:
直线方程为: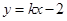 ,设
,设
由
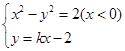 得
得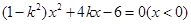
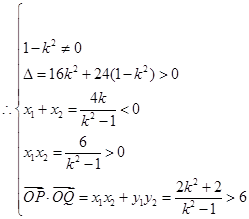 解得:
解得: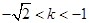
故
 的取值范围为
的取值范围为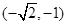
点评:利用圆锥曲线定义求动点的轨迹方程是常出现的考点,要注意的是动点轨迹是整条圆锥曲线还是其中一部分

练习册系列答案
相关题目
 为圆
为圆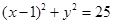 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与

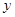 轴相切的圆的标准方程是
轴相切的圆的标准方程是
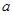 ,
,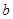 ,
,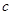 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线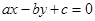 被圆
被圆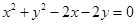 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.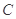 :
: 关于直线
关于直线 对称,则
对称,则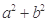 的最小值是( )
的最小值是( )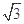


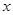 轴相切,圆心在直线
轴相切,圆心在直线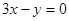 上,且被直线
上,且被直线 所截得的弦长为
所截得的弦长为 ,求此圆方程。
,求此圆方程。 ,直线
,直线 ,求与圆
,求与圆 相切,且与直线
相切,且与直线 垂直的直线方程。
垂直的直线方程。 ,则这个圆的方程是( )
,则这个圆的方程是( )