题目内容
已知圆 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 相切.
相切.
(1)求直线 的方程;
的方程;
(2)设圆 与
与 轴交于
轴交于 两点,
两点, 是圆
是圆 上异于
上异于 的任意一点,过点
的任意一点,过点 且与
且与 轴垂直的直线为
轴垂直的直线为 ,直线
,直线 交直线
交直线 于点
于点 ,直线
,直线 交直线
交直线 于点
于点 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标.
 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 相切.
相切.(1)求直线
 的方程;
的方程;(2)设圆
 与
与 轴交于
轴交于 两点,
两点, 是圆
是圆 上异于
上异于 的任意一点,过点
的任意一点,过点 且与
且与 轴垂直的直线为
轴垂直的直线为 ,直线
,直线 交直线
交直线 于点
于点 ,直线
,直线 交直线
交直线 于点
于点 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标.(1)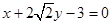 或
或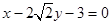
(2)过定点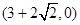 和
和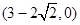
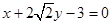 或
或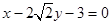
(2)过定点
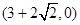 和
和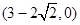
试题分析:(1)设直线
 的方程为
的方程为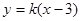 ,即
,即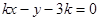 .
. 直线
直线 与圆
与圆 相切,
相切, 圆心
圆心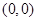 到直线
到直线 的距离
的距离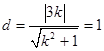 .
.解得
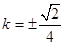 .
. 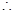 直线
直线 的方程为
的方程为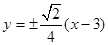 ,
,即
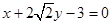 或
或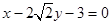 ……………4分
……………4分(2)设直线
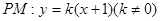 ,
, ,故直线
,故直线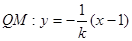
令
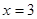 ,可得
,可得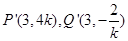 . ………6分
. ………6分 ,故
,故 的外接圆即以
的外接圆即以 为直径的圆.
为直径的圆.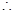 该圆的方程为
该圆的方程为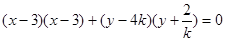
即
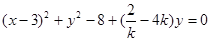 ……………8分
……………8分由此可知,无论
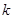 为何值,当
为何值,当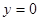 时,总有
时,总有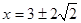
故该圆必过定点
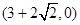 和
和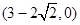 ………10分
………10分点评:解决该试题的关键是利用线与圆的位置关系,结合点到直线的距离公式,得到直线方程,同时利用线线的垂直关系,得到点的坐标,来分析定点。体现了解析几何中运用代数的思想解决解析几何的本质,属于中档题。

练习册系列答案
相关题目
 上有且只有两个点到直线
上有且只有两个点到直线 的取值范围是( )
的取值范围是( )

 的方程为:
的方程为: .
. 的值,使圆
的值,使圆 的直线方程.
的直线方程.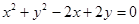 的周长是( )
的周长是( )



 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与

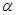 与球O相交于周长为
与球O相交于周长为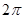 的⊙
的⊙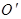 ,A、B为⊙
,A、B为⊙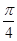 ,且A、B的球面距离为
,且A、B的球面距离为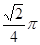 ,则
,则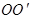 的长度为( )
的长度为( )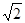 C.
C.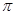 D.2
D.2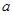 ,
,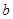 ,
,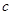 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线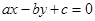 被圆
被圆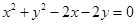 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.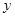 轴上,且与直线
轴上,且与直线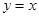 相切于点
相切于点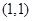 的圆的方程为____________________.
的圆的方程为____________________.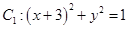 ,圆
,圆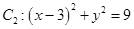 同时外切的动圆圆心的轨迹方程是_____________。
同时外切的动圆圆心的轨迹方程是_____________。