题目内容
(本小题满分14分)
已知方程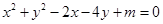 .
.
(1)若此方程表示圆,求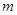 的取值范围;
的取值范围;
(2)若(1)中的圆与直线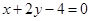 相交于
相交于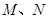 两点,且
两点,且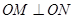 (
(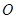 为坐标原点)求
为坐标原点)求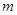 的值;
的值;
(3)在(2)的条件下,求以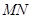 为直径的圆的方程.
为直径的圆的方程.
已知方程
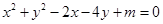 .
.(1)若此方程表示圆,求
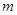 的取值范围;
的取值范围;(2)若(1)中的圆与直线
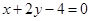 相交于
相交于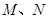 两点,且
两点,且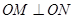 (
(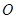 为坐标原点)求
为坐标原点)求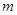 的值;
的值;(3)在(2)的条件下,求以
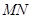 为直径的圆的方程.
为直径的圆的方程.(1)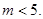 (2)
(2)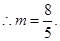 (3)
(3)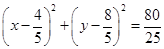
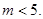 (2)
(2)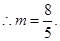 (3)
(3)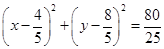
试题分析:解:(1)
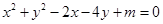
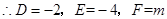
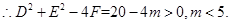 …………3分
…………3分(2)设
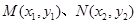 ,由
,由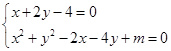 得:
得: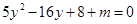
由韦达定理得:
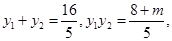
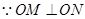 ,
,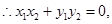
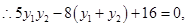
即:
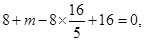
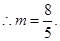 …………10分
…………10分(3)设圆心为
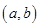 则:
则: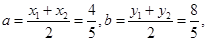 半径
半径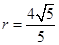
圆的方程为
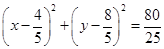 . …………14分
. …………14分点评:解决该试题的关键是利用联立方程组得到根与系数的关系,同时结合向量的数量积为零来表示垂直,得到方程,求解结论,属于中档题。

练习册系列答案
相关题目
 经过点
经过点 和
和 ,且圆心
,且圆心 上,则圆
上,则圆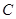 与直线
与直线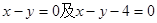 都相切,圆心在直线
都相切,圆心在直线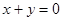 上,则圆
上,则圆
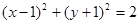


 为圆
为圆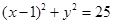 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。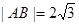 ,求a的值;
,求a的值; O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与

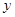 轴相切的圆的标准方程是
轴相切的圆的标准方程是
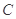 :
: 关于直线
关于直线 对称,则
对称,则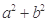 的最小值是( )
的最小值是( )