题目内容
(本小题满分12分)
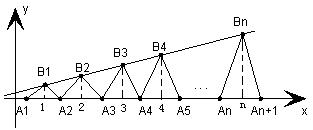
已知点列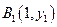 、
、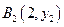 、…、
、…、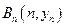 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数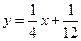 图像上的点,点列
图像上的点,点列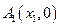 、
、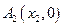 、…、
、…、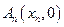 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中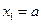 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点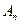 、
、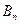 、
、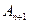 构成一个顶角的顶点为
构成一个顶角的顶点为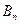 的等腰三角形。
的等腰三角形。
(1)数列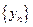 的通项公式,并证明
的通项公式,并证明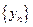 是等差数列;
是等差数列;
(2)证明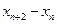 为常数,并求出数列
为常数,并求出数列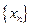 的通项公式;
的通项公式;
(3)上述等腰三角形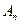
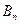
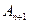 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
已知点列
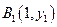 、
、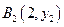 、…、
、…、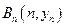 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数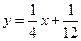 图像上的点,点列
图像上的点,点列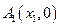 、
、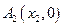 、…、
、…、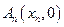 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中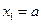 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点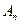 、
、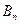 、
、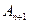 构成一个顶角的顶点为
构成一个顶角的顶点为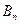 的等腰三角形。
的等腰三角形。
(1)数列
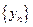 的通项公式,并证明
的通项公式,并证明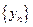 是等差数列;
是等差数列;(2)证明
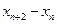 为常数,并求出数列
为常数,并求出数列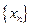 的通项公式;
的通项公式;(3)上述等腰三角形
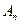
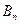
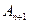 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。(1)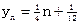 (nÎN),证明见解析
(nÎN),证明见解析
(2)证明见解析,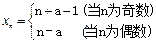
(3)存在直角三形,此时a的值为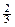 、
、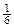 、
、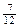 .
.
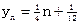 (nÎN),证明见解析
(nÎN),证明见解析(2)证明见解析,
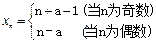
(3)存在直角三形,此时a的值为
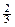 、
、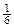 、
、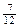 .
.(1)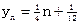 (nÎN),∵yn+1-yn=
(nÎN),∵yn+1-yn=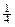 ,∴{yn}为等差数列 ………………4分
,∴{yn}为等差数列 ………………4分
(2)因为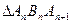 与
与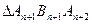 为等腰三角形.
为等腰三角形.
所以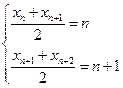 ,两式相减得
,两式相减得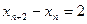 。………………7分
。………………7分
注:判断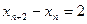 得2分,证明得1分
得2分,证明得1分
∴x1,x3,x5,…,x2n-1及x2,x4,x6 ,…,x2n都是公差为2的等差数列,………………6分
∴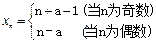 ………………10分
………………10分
(3)要使AnBnAn+1为直角三形,则 |AnAn+1|=2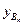 =2(
=2(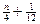 )Þxn+1-xn=2(
)Þxn+1-xn=2(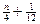 )
)
当n为奇数时,xn+1=n+1-a,xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2(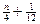 ) Þa=
) Þa=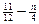 (n为奇数,0<a<1) (*)
(n为奇数,0<a<1) (*)
取n=1,得a=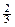 ,取n=3,得a=
,取n=3,得a=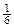 ,若n≥5,则(*)无解; ………………14分
,若n≥5,则(*)无解; ………………14分
当偶数时,xn+1=n+a,xn=n-a,∴xn+1-xn=2a.
∴2a=2(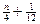 )Þa=
)Þa=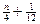 (n为偶数,0<a<1) (*¢),
(n为偶数,0<a<1) (*¢),
取n=2,得a=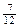 ,若n≥4,则(*¢)无解.
,若n≥4,则(*¢)无解.
综上可知,存在直角三形,此时a的值为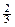 、
、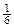 、
、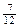 . ………………18分
. ………………18分
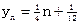 (nÎN),∵yn+1-yn=
(nÎN),∵yn+1-yn=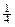 ,∴{yn}为等差数列 ………………4分
,∴{yn}为等差数列 ………………4分(2)因为
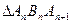 与
与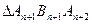 为等腰三角形.
为等腰三角形.所以
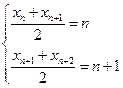 ,两式相减得
,两式相减得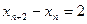 。………………7分
。………………7分注:判断
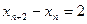 得2分,证明得1分
得2分,证明得1分∴x1,x3,x5,…,x2n-1及x2,x4,x6 ,…,x2n都是公差为2的等差数列,………………6分
∴
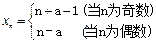 ………………10分
………………10分(3)要使AnBnAn+1为直角三形,则 |AnAn+1|=2
 =2(
=2(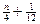 )Þxn+1-xn=2(
)Þxn+1-xn=2(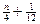 )
)当n为奇数时,xn+1=n+1-a,xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2(
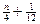 ) Þa=
) Þa=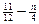 (n为奇数,0<a<1) (*)
(n为奇数,0<a<1) (*)取n=1,得a=
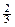 ,取n=3,得a=
,取n=3,得a=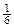 ,若n≥5,则(*)无解; ………………14分
,若n≥5,则(*)无解; ………………14分当偶数时,xn+1=n+a,xn=n-a,∴xn+1-xn=2a.
∴2a=2(
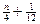 )Þa=
)Þa=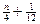 (n为偶数,0<a<1) (*¢),
(n为偶数,0<a<1) (*¢),取n=2,得a=
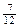 ,若n≥4,则(*¢)无解.
,若n≥4,则(*¢)无解.综上可知,存在直角三形,此时a的值为
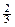 、
、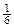 、
、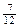 . ………………18分
. ………………18分
练习册系列答案
相关题目
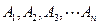 为集合
为集合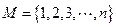 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于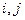 满足下列条件:
满足下列条件: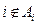 ,且每一个
,且每一个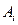 至
至 少含有三个元素;
少含有三个元素;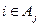 的充要条件是
的充要条件是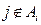 (其中
(其中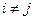 )。
)。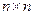 数表),规定第
数表),规定第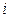 行第
行第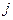 列数为:
列数为: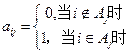 。
。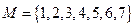 ,请完成下面
,请完成下面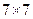 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);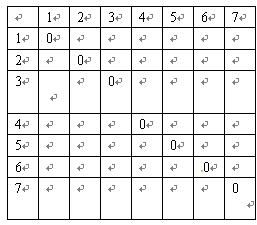
 中1的个数
中1的个数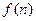 ,并证明
,并证明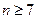 ;
;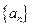 前
前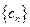 的通项公式为:
的通项公式为: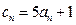 ,证明不等式:
,证明不等式: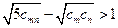 对任何正整数
对任何正整数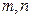 都成立。
都成立。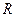 上的函数
上的函数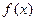 和数列
和数列 满足下列条件:
满足下列条件: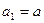 ,
,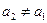 ,当
,当 且
且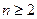 时,
时,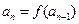 且
且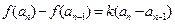 .
.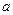 、
、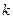 均为非零常数.
均为非零常数.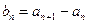
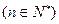 ,若
,若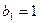 ,求数列
,求数列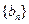 的通项公式;
的通项公式;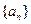 的前
的前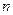 项和为
项和为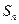 ,且点
,且点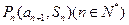 在函数
在函数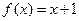 的图象上.
的图象上.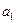 的值;
的值;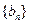 满足:
满足: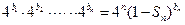 ,且
,且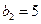 .求数列
.求数列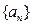 是等差数列,其前n项和为
是等差数列,其前n项和为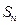 ,已知
,已知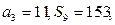 求数列
求数列
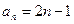 ,数列
,数列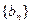 的前n项和为
的前n项和为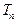 ,满足
,满足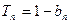
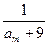 是
是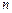 个图形包含
个图形包含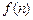 个“福娃迎迎”,
个“福娃迎迎”, ;
; ____________.(答案用数字或
____________.(答案用数字或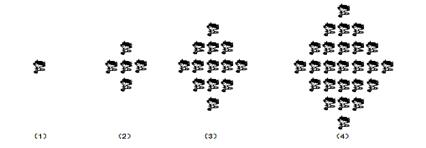
 的前n项和为
的前n项和为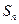 ,若
,若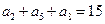 , 则
, 则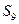 =
= ( ).
( ).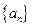 中,
中,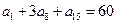 ,则
,则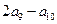 的值为
的值为