题目内容
在数列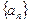 中,已知
中,已知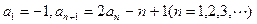
(1)证明数列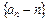 是等比数列
是等比数列
(2)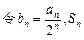 为数列
为数列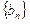 的前
的前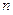 项和,求
项和,求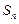 的表达式
的表达式
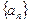 中,已知
中,已知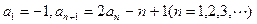
(1)证明数列
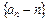 是等比数列
是等比数列(2)
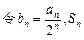 为数列
为数列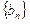 的前
的前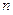 项和,求
项和,求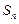 的表达式
的表达式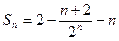
(1)解: ∵
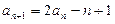 , ∴
, ∴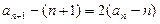 ,
,∴
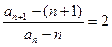 , 又
, 又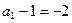 ,
,∴ 数列
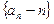 是以2为公比、以-2为首项的等比数列.…………… 6分
是以2为公比、以-2为首项的等比数列.…………… 6分(2)由(1)得:
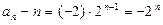 , ∴
, ∴  ,
,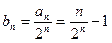 ,
,∴
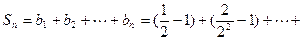
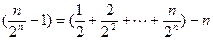 ,
,令
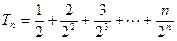 , 则
, 则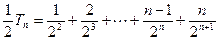 ,
,两式相减得:
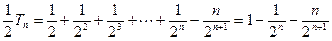
∴
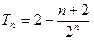 , 即
, 即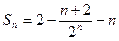 . ………………………12分
. ………………………12分
练习册系列答案
相关题目
题目内容
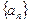 中,已知
中,已知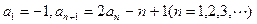
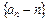 是等比数列
是等比数列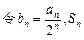 为数列
为数列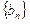 的前
的前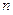 项和,求
项和,求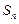 的表达式
的表达式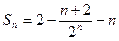
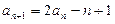 , ∴
, ∴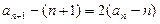 ,
,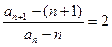 , 又
, 又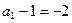 ,
,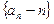 是以2为公比、以-2为首项的等比数列.…………… 6分
是以2为公比、以-2为首项的等比数列.…………… 6分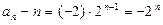 , ∴
, ∴  ,
,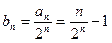 ,
,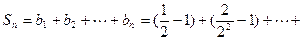
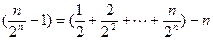 ,
,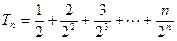 , 则
, 则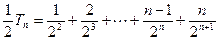 ,
,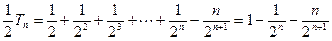
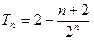 , 即
, 即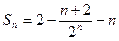 . ………………………12分
. ………………………12分