题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为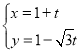 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)在曲线![]() 的极坐标方程中,由
的极坐标方程中,由![]() ,
,![]() 可将曲线
可将曲线![]() 的极坐标方程化为直角坐标方程,在直线
的极坐标方程化为直角坐标方程,在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() ,可得出直线
,可得出直线![]() 的普通方程;
的普通方程;
(2)将直线![]() 的参数方程表示为
的参数方程表示为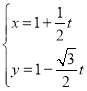 (
(![]() 为参数),并设点
为参数),并设点![]() 、
、![]() 对应的参数分别为
对应的参数分别为![]() 、
、![]() ,将直线
,将直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的普通方程联立,得出关于
的普通方程联立,得出关于![]() 的二次方程,并列出韦达定理,可计算出
的二次方程,并列出韦达定理,可计算出![]() 的值.
的值.
(1)在曲线![]() 的极坐标方程中,由
的极坐标方程中,由![]() ,
,![]() 可得出曲线
可得出曲线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() .
.
在直线![]() 的参数方程中消去
的参数方程中消去![]() 得
得![]() ,即
,即![]() ;
;
(2)直线![]() 的参数方程表示为
的参数方程表示为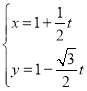 (
(![]() 为参数),
为参数),
并设点![]() 、
、![]() 对应的参数分别为
对应的参数分别为![]() 、
、![]() ,
,
将直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的直角坐标方程联立,消去
的直角坐标方程联立,消去![]() 、
、![]() 得
得![]() .
.
由韦达定理得![]() ,
,![]() .
.
因此,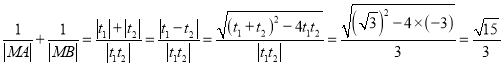 .
.

练习册系列答案
相关题目
【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: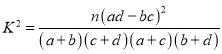 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |