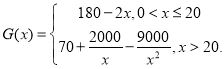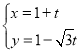题目内容
【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: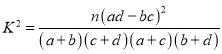 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)![]() ;(2)有
;(2)有![]() 的把握认为相关.
的把握认为相关.
【解析】
(1)首先补全列联表,用频率估计概率得到以看书为休闲方式的男性的概率,
记这3人中至少有1人是以看书为休闲方式的为事件![]() ,则事件
,则事件![]() 的对立事件为这3人中没有1人是以看书为休闲方式,根据相互独立事件的概率公式计算可得;
的对立事件为这3人中没有1人是以看书为休闲方式,根据相互独立事件的概率公式计算可得;
(2)首先求出卡方,再跟参考数据比较即可得出结论;
解:(1)依题意,补全以上列联表
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
用频率估计概率,可得以看书为休闲方式的男性的概率为![]()
则随机调查3名在该社区的男性,记这3人中至少有1人是以看书为休闲方式的为事件![]() ,
,
则事件![]() 的对立事件为这3人中没有1人是以看书为休闲方式其概率为
的对立事件为这3人中没有1人是以看书为休闲方式其概率为![]() ,
,
所以![]()
(2)由(1)中的列联表可得![]() ,
,
![]() 的概率约为0.01,所以我们有
的概率约为0.01,所以我们有![]() 的把握认为相关.
的把握认为相关.

 寒假学与练系列答案
寒假学与练系列答案【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.