题目内容

6．已知函数y=log${\;}_{\frac{1}{2}}$（ax2+2x+1）的值域为x+2y+4=4xy，则实数a的取值范围是[0，1]．

分析 若函数y=log${\;}_{\frac{1}{2}}$（ax2+2x+1）的值域为R，则ax2+2x+1的值域须含有一切正实数，对a进行分类讨论，可得答案．

解答 解：若函数y=log${\;}_{\frac{1}{2}}$（ax2+2x+1）的值域为R，
则ax2+2x+1的值域须含有一切正实数，
（1）当a=0时，ax2+2x+1=2x+1含有一切正实数集，符合题意；
（2）当a≠0，须有$\left\{{\begin{array}{l}{a＞0}\\{△=4-4a≥0}\end{array}}\right.$，解得0＜a≤1．
综上所述，实数a的取值范围是0≤a≤1．
即实数a的取值范围是[0，1]，
故答案为[0，1]．

点评 本题考查的知识点是对数函数的图象与性质，其中根据已知分析出ax2+2x+1的值域须含有一切正实数，是解答的关键．

练习册系列答案
相关题目
17．已知全集U=R，集合A={y|y=2x，x∈R}，B={x|x≥2}，则下图中阴影部分所表示的集合为（　　）
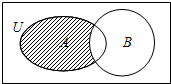
A．∅B．{0，1}C．（0，2）D．（-∞，2）
18．i为虚数单位，则${（{\frac{1+i}{1-i}}）^7}$=-i．
15．已知命题p：设a，b∈R，则“a+b＞4”是“a＞2且b＞2”的必要不充分条件；
命题q：“?x0∈R，使得x02-x0＞0”的否定是：“?x∈R，均有x2-x＜0”；
在命题①p∧q；②（?p）∨（?q）；③p∨（?q）； ④（?p）∨q中，真命题的序号是（　　）
A．①③B．①④C．②③D．②④
1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的中心为坐标原点，离心率e=$\frac{\sqrt{6}}{3}$，A1，A2，B1，B2是其四个顶点，且四边形A1B1A2B2的面积为4$\sqrt{3}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过椭圆C的右焦点F且与椭圆C相交于M，N两点的直线l，使得在直线x=3上可以找到一点B，满足△MNB为正三角形？若存在，求出直线l的方程；若不存在，请说明理由．
11．设函数f（x）=xlnx．
（Ⅰ） 求f（x）的极值；
（Ⅱ）设g（x）=f（x+1），若对任意的x≥0，都有g（x）≥mx成立，求实数m的取值范围；
（Ⅲ）若0＜a＜b，证明：$0＜f（a）+f（b）-2f（\frac{a+b}{2}）＜（b-a）ln2$．
18．在如图所示的程序框图中，若输出的S值等于16，则在该程序框图中的判断框内填写的条件为（　　）
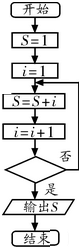
A．i＞5B．i＞6C．i＞7D．i＞8
15．错位相减法求和：an=（2n+1）•3n，求Sn．
16．某同学为了计算函数y=lnx图象与x轴，直线x=1，x=e所围成形状A的面积，采用“随机模拟方法”，用计算机分别产生10个在[1，e]上的均匀随机数xi（1≤i≤10）和10个在[0，1]上的均匀随机数yi（1≤i≤10），其数据记录为如下表的前两行．
xi2.50 1.01 1.90 1.22 2.52 2.17 1.89 1.96 1.36 2.22
yi0.84 0.25 0.98 0.15 0.01 0.60 0.59 0.88 0.84 0.10
lnxi0.92 0.01 0.64 0.20 0.92 0.77 0.64 0.67 0.31 0.80
（1）依次表格中的数据回答，在图形A内的点有多少个，分别是什么？
（2）估算图形A的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网