题目内容
16.某同学为了计算函数y=lnx图象与x轴,直线x=1,x=e所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行.| xi | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| yi | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnxi | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
(2)估算图形A的面积.
分析 (1)根据题意,画出图形,利用图形得出条件yi<lnxi,由此求出表格中的数据在图形A内的点有几个;
(2)利用几何概型得出$\frac{{∫}_{1}^{e}lnxdx}{e-1}$=$\frac{6}{10}$,求出${∫}_{1}^{e}$lnxdx的值即可.
解答 解:(1)根据题意,画出图形,如图所示;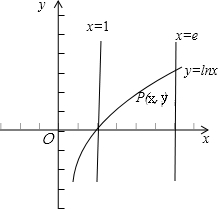
由yi<lnxi得,
表格中的数据满足条件的点,即在图形A内的点有6个,
分别是(2.50,0.84),(1.22,0.20),(2.52,0.01),
(2.17,0.60),(1.89,o.59),(2.22,0.10);
(2)由(1)知,表中10个点(xi,yi)满足yi≤f(xi)的点有6个,
∴$\frac{{∫}_{1}^{e}lnxdx}{e-1}$=$\frac{6}{10}$=$\frac{3}{5}$,
即${∫}_{1}^{e}$lnxdx=$\frac{3}{5}$(e-1);
∴估计图形A的面积为$\frac{3}{5}$(e-1).
点评 本题考查了利用几何概型模拟估计定积分的值,以及定积分在面积中的简单应用问题,是基础题目.

练习册系列答案
相关题目
11.当-$\frac{π}{2}$<x<$\frac{π}{2}$时,函数y=lg|x|的图象是( )
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 不是对称图形 |
8.已知函数f(x)=$\frac{x({a}^{x}-1)}{{a}^{x}+1}$(a>0,a≠1),则( )
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | 函数f(x)在(0,+∞)上是减函数 | ||
| C. | 函数f(x)是奇函数 | D. | 函数f(x)是偶函数 |
5.若2sin2($\frac{π}{4}$+$\frac{x}{2}$)=1-cos(π-x),则sin2x=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |