题目内容
11.设函数f(x)=xlnx.(Ⅰ) 求f(x)的极值;
(Ⅱ)设g(x)=f(x+1),若对任意的x≥0,都有g(x)≥mx成立,求实数m的取值范围;
(Ⅲ)若0<a<b,证明:$0<f(a)+f(b)-2f(\frac{a+b}{2})<(b-a)ln2$.
分析 (Ⅰ)求出函数的导数,利用函数的单调性求解函数的极值即可.
(Ⅱ)求出g(x)的解析式,构造函数令h(x)=(x+1)ln(x+1)-mx,通过导函数的符号,求解实数m的取值范围.
(III)构造函数$F(x)=alna+xlnx-(a+x)ln\frac{a+x}{2}$,x>a,通过导函数的符号,集合函数的单调性求解函数的极值,推出结果即可.
解答 (本小题满分14分)
解:(Ⅰ)函数f(x)=xlnx,则f′(x)=1+lnx,(x>0)
令f′(x)=0,解得:$x=\frac{1}{e}$,且当$x∈(0,\frac{1}{e})$时,f′(x)<0,$x∈(\frac{1}{e},+∞)$时,f′(x)>0
因此:f(x)的极小值为$f(\frac{1}{e})=-\frac{1}{e}$
(Ⅱ)g(x)=f(x+1)=(x+1)ln(x+1)
令h(x)=(x+1)ln(x+1)-mx,则h′(x)=ln(x+1)+1-m
注意到:h(0)=0,若要h(x)≥0,必须要求h'(0)≥0,即1-m≥0,亦即m≤1
另一方面:当m≤1时,h′(x)=ln(x+1)+1-m≥0恒成立;
故实数m的取值范围为:m≤1
(III)构造函数$F(x)=alna+xlnx-(a+x)ln\frac{a+x}{2}$,x>a,$F'(x)=1+lnx-ln\frac{a+x}{2}-1=ln\frac{2x}{a+x}$,
∵x>a,∴0<a+x<2x,F′(x)>0,F(x)在(a,+∞)上是单调递增的;
故F(b)>F(a)=0,即:$f(a)+f(b)-2f(\frac{a+b}{2})>0$
另一方面,构造函数$G(x)=alna+xlnx-(a+x)ln\frac{a+x}{2}-(x-a)ln2$,
$G'(x)=ln\frac{2x}{a+x}-ln2=ln\frac{x}{a+x}<0$,
G(x)在(a,+∞)上是单调递减的
故G(b)<G(a)=0即:$f(a)+f(b)-2f(\frac{a+b}{2})<(b-a)ln2$
综上,$0<f(a)+f(b)-2f(\frac{a+b}{2})<(b-a)ln2$.
点评 本题考查好的导数的应用,函数的极值以及函数的单调性,考查分析问题解决问题的能力,构造法的应用,考查转化思想以及计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | 充分必要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
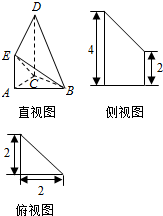 若如图为某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧视图、俯视图,则其正视图的面积为4,三棱锥D-BCE的体积为$\frac{8}{3}$.
若如图为某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧视图、俯视图,则其正视图的面积为4,三棱锥D-BCE的体积为$\frac{8}{3}$.