题目内容
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 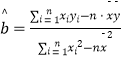 ,
, ![]() .
.
【答案】
(1)解:由题所给的数据样本平均数 ![]() =
= ![]() (1+2+3+4+5+6+7)=4,
(1+2+3+4+5+6+7)=4,
![]() =
= ![]() (2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3.
(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3.
∴ 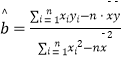 =
= ![]() =0.5,
=0.5,
![]() =4.4﹣0.5×4=2.4,
=4.4﹣0.5×4=2.4,
∴y关于x的线性回归方程为:y=0.5x+2.4.
(2)解:由(Ⅰ)可得线性回归方程为y=0.5x+2.4.
∵0.5>0,
故2010年至2016年该市新开楼盘平均销售价格逐年增加
2018年的年份代号x=9,可得y=0.5×9+2.4=6.9(千元).
即预测该市2018年新开楼盘的平均销售价格为每平方6.9千元
【解析】1、根据题意可得由公式求出![]() ,
, ![]() 即可得到结论。
即可得到结论。
2、利用(1)的线性回归方程代入x=9即可。

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目