题目内容
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若a=0时,求函数y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在[1,2]上是减函数,求实数a的取值范围.
【答案】
(1)解:若a=0时,f(x)=x2﹣lnx的导数为f′(x)=2x﹣ ![]() ,
,
函数y=f(x)在点(1,f(1))处的切线斜率为k=2﹣1=1,切点为(1,1),
则有切线方程为y﹣1=x﹣1,即为x﹣y=0
(2)解:∵函数f(x)在[1,2]内是减函数,
∴f'(x)= ![]() ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,
令h(x)=2x2+ax﹣1,有 ![]() 得
得 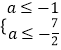 ,
,
∴a≤﹣ ![]()
【解析】(1)求出a=0时函数的导数,求得切线的斜率和切点,由点斜式方程即可得到切线方程;(2)先对函数f(x)进行求导,根据函数f(x)在[1,2]上是减函数可得到其导函数在[1,2]上小于等于0应该恒成立,再结合二次函数的性质可求得a的范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 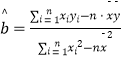 ,
, ![]() .
.