题目内容
【题目】求证:点 P(x0,y0) 到直线Ax+By+C=0的距离为![]()
【答案】证明:设Q(x,y) 是直线上任意一点,则 Ax+By+C=0 .因为|PQ|2=(x-x0)2+(y-y0)2, ![]() ,由柯西不等式,得
,由柯西不等式,得![]()
![]()
![]()
![]()
所以![]() .
.
当且仅当![]() 时,取等号,|PQ| 取得最小值
时,取等号,|PQ| 取得最小值 ![]() .
.
因此,点 P(x0,y0) 到直线Ax+By+C =0的距离为 ![]() .
.
【解析】本题主要考查了二维形式的柯西不等式,解决问题的关键是利用二维形式的柯西不等式 ![]() ,取“=”的条件是ad=bc.因此,在解题时,对照柯西不等式,必须弄清要求的问题中相当于柯西不等式中的“a , b , c , d”的数或代数式,否则一般出错.
,取“=”的条件是ad=bc.因此,在解题时,对照柯西不等式,必须弄清要求的问题中相当于柯西不等式中的“a , b , c , d”的数或代数式,否则一般出错.
【考点精析】本题主要考查了二维形式的柯西不等式的相关知识点,需要掌握二维形式的柯西不等式:![]() 当且仅当
当且仅当![]() 时,等号成立才能正确解答此题.
时,等号成立才能正确解答此题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 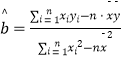 ,
, ![]() .
.