题目内容
【题目】已知圆C：x2+y2+Dx+Ey+3=0，圆心在直线x+y﹣1=0上，且圆心在第二象限，半径长为 
，求圆的一般方程．
【答案】解：将圆C化成标准方程，得（x+ 
）2+（y+ 
）2= 
（D2+E2﹣12）
∴圆C的圆心坐标为（﹣ ，﹣ ），半径r= 
∵圆C关于直线x+y﹣1=0对称，半径为 
．
∴﹣ ﹣ ﹣1=0且 = ，
解之得 
或 
．
结合圆心C在第二象限，得C的坐标为（﹣1，2），（舍去C（1，﹣2））
∴圆C的方程是（x+1）2+（y﹣2）2=2，
∴圆的一般方程为x2+y2+2x﹣4y+3=0．
【解析】将圆C的一般方程化为标准方程，得到圆心坐标和半径，将圆心坐标代入直线方程，结合圆心在第二象限，即可得到圆心坐标，从而得到圆的一般方程.
【考点精析】本题主要考查了圆的一般方程的相关知识点，需要掌握圆的一般方程的特点：(1)①x2和y2的系数相同，不等于0．②没有xy这样的二次项；(2)圆的一般方程中有三个特定的系数D、E、F，因之只要求出这三个系数，圆的方程就确定了；(3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指出了圆心坐标与半径大小，几何特征较明显才能正确解答此题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】某市2010年至2016年新开楼盘的平均销售价格y（单位：千元/平米）的统计数据如表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
（1）求y关于x的线性回归方程；
（2）利用（Ⅰ）中的回归方程，分析2010年至2016年该市新开楼盘平均销售价格的变化情况，并预测该市2018年新开楼盘的平均销售价格．
附：参考数据及公式： 
， 
， 
．
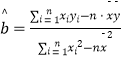