题目内容
【题目】已知f(x)=3x2﹣2x,数列{an}的前n项和为Sn , 点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
【答案】
(1)解:∵f(x)=3x2﹣2x,数列{an}的前n项和为Sn,
点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴ ![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1=(3n2﹣2n)﹣[3(n﹣1)2﹣2(n﹣1)]=6n﹣5,
当n=1时,a1=S1=3﹣2=1,满足上式,
∴an=6n﹣5,n∈N*.的
(2)解:由(1)得 ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]()
= ![]() ,
,
∴使得Tn< ![]() 对所有n∈N*都成立的最小正整数m必须且仅须满足
对所有n∈N*都成立的最小正整数m必须且仅须满足 ![]() ,
,
即m≥10,∴满足要求的最小整数m=10.
【解析】1、利用点在直线上可得到S n = 3 n2 2 n,根据an和 Sn关系式求出 an=6n﹣5。
2、根据(1)的结论可得出数列{bn}的通项公式,求出 Tn 的式子用列项相消法得到 ![]()
![]() ,再由放缩法得到这个式子小于
,再由放缩法得到这个式子小于![]() ,由已知可求得
,由已知可求得 ![]() ≤
≤ ![]() ,故得结果。
,故得结果。
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系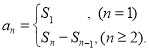 即可以解答此题.
即可以解答此题.

【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 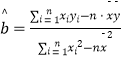 ,
, ![]() .
.