题目内容
【题目】已知函数![]() .用反证法证明方程f(x)=0 没有负数根.
.用反证法证明方程f(x)=0 没有负数根.
【答案】证明:证法一:假设存在x0<0(x0≠-1)满足f(x0)=0,
则 ![]() ,且
,且![]() ,
,
∴ ![]() ,即
,即![]() .
.
与假设x0<0矛盾,故方程f(x)=0没有负数根.
证法二:假设存在x0<0(x0≠-1)满足f(x0)=0.
①若-1<x0<0,则![]() ,
, ![]() ,
,
∴f(x0<-1,与f(x0)=0矛盾;
②若x0<-1,则![]() ,
, ![]() ,
,
∴f(x0)>0,与f(x0)=0矛盾.
故方程f(x)=0没有负数根.
【解析】本题主要考查了反证法与放缩法,解决问题的关键是假设存在x0<0(x0≠-1)满足f(x0)=0,如何得到与已知的矛盾即可.
【考点精析】本题主要考查了反证法与放缩法的相关知识点,需要掌握常见不等式的放缩方法:①舍去或加上一些项②将分子或分母放大(缩小)才能正确解答此题.

练习册系列答案
相关题目
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 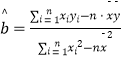 ,
, ![]() .
.