题目内容
【题目】已知函数f(x)=(x﹣a)cosx﹣sinx,g(x)![]() x3
x3![]() ax2,a∈R
ax2,a∈R
(1)当a=1时,求函数y=f(x)在区间(0,![]() )上零点的个数;
)上零点的个数;
(2)令F(x)=f(x)+g(x),试讨论函数y=F(x)极值点的个数.
【答案】(1)零点的个数为0,(2)无极值.
【解析】
(1)结合函数![]() 的单调性和极值,即可得到本题答案;
的单调性和极值,即可得到本题答案;
(2)先求导,再分类讨论,即可得到![]() 的单调区间和极值,由此即可得到本题答案.
的单调区间和极值,由此即可得到本题答案.
(1)当![]() 时,
时,![]() ,
,
∴![]() ,
,
因为当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,函数取得最大值
时,函数取得最大值![]() ,
,
所以函数![]() 在区间
在区间![]() 上零点的个数为0;
上零点的个数为0;
(2)![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为增函数,又
上为增函数,又![]() ,
,
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
①若![]() 时,
时,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递减,
上单调递减,
故有2个极值;
②若![]() 时,
时,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递减,
上单调递减,
故有2个极值点;
③当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在R上单调递增,无极值点.
在R上单调递增,无极值点.

【题目】为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,画出频率分布直方图(如图所示).
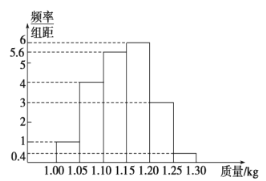
(1)在下面表格中填写相应的频率;
分组 | 频率 |
| |
| |
| |
| |
| |
|
(2)估计数据落在![]() 中的概率;
中的概率;
(3)将上面捕捞的100条鱼分别作一记分组频率号后再放回水库.几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条.请根据这一情况来估计该水库中鱼的总条数.
【题目】某商场为改进服务质量,在进场购物的顾客中随机抽取了![]() 人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
满意 | 不满意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握认为顾客购物体验的满意度与性别有关?
的把握认为顾客购物体验的满意度与性别有关?
![]() 若在购物体验满意的问卷顾客中按照性别分层抽取了
若在购物体验满意的问卷顾客中按照性别分层抽取了![]() 人发放价值
人发放价值![]() 元的购物券.若在获得了
元的购物券.若在获得了![]() 元购物券的
元购物券的![]() 人中随机抽取
人中随机抽取![]() 人赠其纪念品,求获得纪念品的
人赠其纪念品,求获得纪念品的![]() 人中仅有
人中仅有![]() 人是女顾客的概率.
人是女顾客的概率.
附表及公式: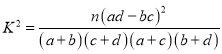 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
