题目内容
【题目】已知椭圆![]() ,过原点O且斜率不为0的直线与椭圆C交于P,Q两点.
,过原点O且斜率不为0的直线与椭圆C交于P,Q两点.
(1)若![]() 为椭圆C的一个焦点,求椭圆C的标准方程;
为椭圆C的一个焦点,求椭圆C的标准方程;
(2)若经过椭圆C的右焦点的直线l与椭圆C交于A,B两点,四边形OAPB能否为平行四边形?若能,求此时直线OP的方程,若不能,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)变形 ,根据
,根据![]() 的关系求解即可;
的关系求解即可;
(2)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,根据韦达定理及向量的坐标运算,求得
,代入椭圆方程,根据韦达定理及向量的坐标运算,求得![]() 点坐标,代入椭圆方程,即可求得
点坐标,代入椭圆方程,即可求得![]() 的值.
的值.
解:(1)由已知得 ,则
,则![]() ,解得
,解得![]() ,
,
所以椭圆C的标准方程为![]() ;
;
(2)设![]() ,
,
当直线![]() 的斜率为0时,
的斜率为0时,![]() 三点共线,不符合题意,
三点共线,不符合题意,
所以可设直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,可得
,可得![]() ,
,
显然,![]() ,则
,则![]() ,
,
若四边形![]() 为平行四边形,则
为平行四边形,则![]() ,
,
所以,![]() ,
,![]() ,
,
因为![]() 在椭圆上,所以
在椭圆上,所以![]() ,即
,即 ,
,
解得![]() ,
,
所以四边形![]() 能为平行四边行,此时直线
能为平行四边行,此时直线![]() 的方程为
的方程为![]() 或
或![]() ,
,
综上所述,四边形![]() 能为平行四边形,此时直线
能为平行四边形,此时直线![]() 的方程为
的方程为![]() 或
或![]() .
.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1100名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 40 |
使用其他理财产品 | 60 |
合计 | 1100 |
已知这1100名市民中,使用“余额宝”的人比使用“财富通”的人多200名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() ,“京东小金库”的平均年化收益率为
,“京东小金库”的平均年化收益率为![]() ,有3名市民,每个人理财的资金有10000元,且分别存入“余额宝”“财富通”“京东小金库”,求这3名市民2018年理财的平均年化收益率;
,有3名市民,每个人理财的资金有10000元,且分别存入“余额宝”“财富通”“京东小金库”,求这3名市民2018年理财的平均年化收益率;
(3)若在1100名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取5人,然后从这5人中随机选取2人,求“这2人都使用‘财富通’”的概率.
注:平均年化收益率,也就是我们所熟知的利率,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
(2)已知在试点前分类意识强的![]() 户居民中,有
户居民中,有![]() 户自觉垃圾分类在
户自觉垃圾分类在![]() 年以上,现在从试点前分类意识强的
年以上,现在从试点前分类意识强的![]() 户居民中,随机选出
户居民中,随机选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,求
,求![]() 分布列及数学期望.
分布列及数学期望.
参考公式: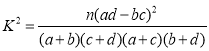 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|