题目内容
己知函数
(1)当 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值;
(2)设 ABC的内角A,B,C的对应边分别为a,b,c,且c=
ABC的内角A,B,C的对应边分别为a,b,c,且c= ,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
(1) 的最小值是
的最小值是 ,最大值是2 ;(2)
,最大值是2 ;(2)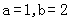 .
.
解析试题分析:(1)化简函数得
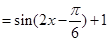 ,
,
根据自变量的范围,确定得到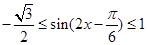 ,从而
,从而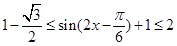 ,得解.
,得解.
(2)由已知,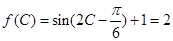 ,可得
,可得 .
.
根据向量 与向量
与向量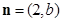 共线,可得
共线,可得 ,
,
应用余弦定理得, 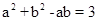 ,即可解得.
,即可解得.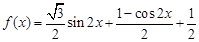

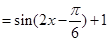 3分
3分
∵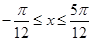 ,∴
,∴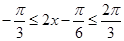 ,
,
∴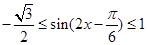 ,从而
,从而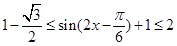
则 的最小值是
的最小值是 ,最大值是2 6分
,最大值是2 6分
(2)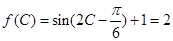 ,则
,则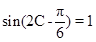 ,
,
∵ ,∴
,∴ ,
,
∴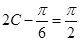 ,解得
,解得 . 8分
. 8分
∵向量 与向量
与向量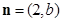 共线,∴
共线,∴ ,
,
即 ① 9分
① 9分
由余弦定理得,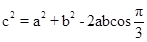 ,即
,即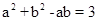 ②
②
由①②解得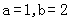 . 12分
. 12分
考点:三角函数式的图象和性质,三角函数式的化简,余弦定理的应用.

练习册系列答案
相关题目
 ,并写出函数
,并写出函数 的最小正周期;
的最小正周期; 为非零常数,且
为非零常数,且 ,试问
,试问 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论. )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π. ]上的单调性.
]上的单调性. 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形 ,使得
,使得 ,
, .
. ,求三角形铁皮
,求三角形铁皮
 -A)+cos(π+A)=-
-A)+cos(π+A)=- .
.
 时,求函数
时,求函数 取得最大值和最小值;
取得最大值和最小值; 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是 ,且
,且 ,若向量
,若向量 与向量
与向量 平行,求
平行,求 的值.
的值. 0,
0, .
. 值; (2)求
值; (2)求 的值.
的值.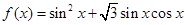 .
. 的值;
的值;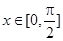 时,求函数
时,求函数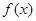 的最大值和最小值.
的最大值和最小值. ,
,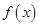 并求
并求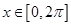 时,求f(x)的最小值以及取得最小值时x的集合.
时,求f(x)的最小值以及取得最小值时x的集合.