题目内容
已知函数
(1)当 时,求函数
时,求函数 取得最大值和最小值;
取得最大值和最小值;
(2)设锐角 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是 ,且
,且 ,若向量
,若向量 与向量
与向量 平行,求
平行,求 的值.
的值.
(1) 时,
时, 取得最大值0;
取得最大值0; 时,
时, 取得最小值
取得最小值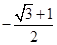 .(2)
.(2) .
.
解析试题分析:(1)将 解析式降次、化一得
解析式降次、化一得
 ,由于
,由于 ,
, ,将
,将 看作一个整体结合正弦函数的图象可得
看作一个整体结合正弦函数的图象可得 .由
.由 得
得 取得最大值0;由
取得最大值0;由 得
得 取得最小值
取得最小值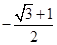 .(2)因为向量
.(2)因为向量 与向量
与向量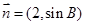 平行,所以
平行,所以 即
即 ,又
,又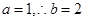 .由余弦定理得
.由余弦定理得 ,这样根据角C的范围便得边
,这样根据角C的范围便得边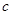 的范围;再据题设
的范围;再据题设 ,即可得
,即可得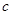 的值.
的值.
(1)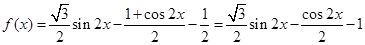
 3分
3分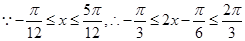
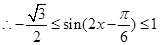 4分
4分
所以当 即
即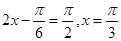 时,
时, 取得最大值0;
取得最大值0;
当 即
即 时,
时, 取得最小值
取得最小值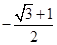 6分
6分
(2)因为向量 与向量
与向量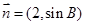 平行,所以
平行,所以 即
即
又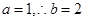 .8分
.8分
由余弦定理
因为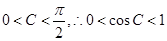 ,
, 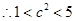 即
即
又因为 ,所以
,所以 ,经检验符合三角形要求 12分
,经检验符合三角形要求 12分
考点:1、三角恒等变换;2、向量与三角形.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 .
. )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.
 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值; ABC的内角A,B,C的对应边分别为a,b,c,且c=
ABC的内角A,B,C的对应边分别为a,b,c,且c= ,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.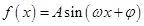 ,x∈R(其中A>0,ω>0,
,x∈R(其中A>0,ω>0,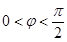 )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M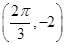 .
. 时,求f(x)的最大值.
时,求f(x)的最大值. 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为 .
. ,求点A的坐标.
,求点A的坐标.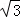 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R) =(
=( ,
,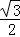 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,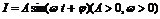 。(1)在一个周期内
。(1)在一个周期内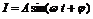 如图所示,试根据图象写出
如图所示,试根据图象写出 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数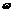 的最小值为多少?
的最小值为多少?