题目内容
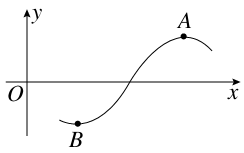
函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A,B分别为该部分图象的最高点与最低点,且这两点间的距离为4 ,则函数f(x)图象的一条对称轴的方程为( )
,则函数f(x)图象的一条对称轴的方程为( )
 ,则函数f(x)图象的一条对称轴的方程为( )
,则函数f(x)图象的一条对称轴的方程为( )
A.x=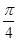 | B.x=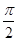 | C.x=4 | D.x=2 |
D
由题意知|AB|=4 ,
,
即最值之差为4,故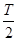 =4,T=8,
=4,T=8,
所以f(x)=2cos(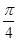 x+φ)(0<φ<π),
x+φ)(0<φ<π),
又f(x)=2cos(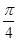 x+φ)(0<φ<π)为奇函数,f(0)=0,
x+φ)(0<φ<π)为奇函数,f(0)=0,
故φ=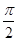 ,令
,令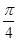 x+
x+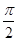 =kπ,k∈Z,
=kπ,k∈Z,
得x=-2+4k,k∈Z,
故x=2是一条对称轴.故选D.
 ,
,即最值之差为4,故
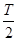 =4,T=8,
=4,T=8,所以f(x)=2cos(
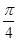 x+φ)(0<φ<π),
x+φ)(0<φ<π),又f(x)=2cos(
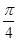 x+φ)(0<φ<π)为奇函数,f(0)=0,
x+φ)(0<φ<π)为奇函数,f(0)=0,故φ=
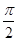 ,令
,令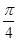 x+
x+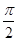 =kπ,k∈Z,
=kπ,k∈Z,得x=-2+4k,k∈Z,
故x=2是一条对称轴.故选D.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
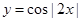 ,②
,②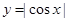 ,③
,③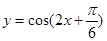 ,④
,④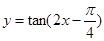 中,最小正周期为
中,最小正周期为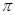 的所有函数为
的所有函数为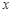 方程
方程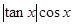 =a在区间
=a在区间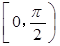
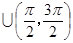 上有两个不同的实根,则实数a的取值范围为__________________.
上有两个不同的实根,则实数a的取值范围为__________________. )的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
)的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )


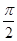 ,
,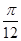 对称,则在下面四个结论中:①图象关于点(
对称,则在下面四个结论中:①图象关于点(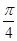 ,0)对称;②图象关于点(
,0)对称;②图象关于点(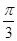 ,0)对称;③在[0,
,0)对称;③在[0,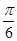 ]上是增函数;④在[-
]上是增函数;④在[-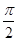 )上的函数y=6cosx的图象与y=5tanx的图象交于点P,过点P作x轴的垂线,垂足为P1,直线PP1与函数y=sinx的图象交于点P2,则线段P1P2的长为________.
)上的函数y=6cosx的图象与y=5tanx的图象交于点P,过点P作x轴的垂线,垂足为P1,直线PP1与函数y=sinx的图象交于点P2,则线段P1P2的长为________. 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为 .
. ,求点A的坐标.
,求点A的坐标.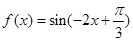 的图像向右平移
的图像向右平移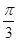 个单位可以得到函数
个单位可以得到函数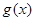 的图像,则
的图像,则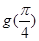 等于( )
等于( )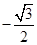
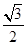
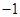
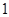
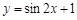 的最小正周期为 .
的最小正周期为 .