题目内容
垂直于x轴的直线交双曲线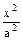 -
-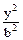 =1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.
=1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.
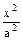 -
-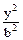 =1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.
=1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.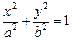
a=b时表示以原点为圆心,a为半径的圆;a>b时,表示焦点在x轴上的椭圆;a<b时,表示焦点在y轴上的椭圆.提示:设出点的坐标,写出直线方程(含参变量),结合点在曲线上,消去参数.

练习册系列答案
相关题目
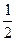 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 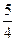 ),抛物线C:
),抛物线C: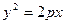 (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.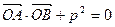 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.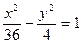
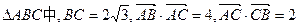 ,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
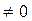 使|OF|=|OG|
使|OF|=|OG|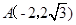 ,B(,-),则
,B(,-),则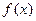 在定义域(-1,1)内可导,且
在定义域(-1,1)内可导,且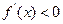 ,点A(1,
,点A(1,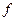 (
(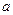 ));B(
));B(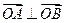 成立,试在
成立,试在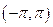 内求满足不等式
内求满足不等式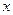 cos
cos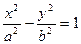 的离心率为
的离心率为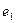 ,双曲线
,双曲线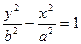 的离心率为
的离心率为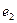 ,则
,则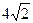
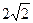
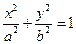
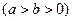 的左、右焦点分别为
的左、右焦点分别为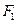 、
、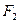 ,抛物线
,抛物线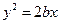 的焦点为
的焦点为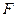 .若
.若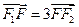 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )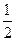 B.
B.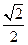 C.
C.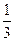 D.
D.