题目内容
若
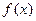 在定义域(-1,1)内可导,且
在定义域(-1,1)内可导,且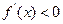 ,点A(1,
,点A(1,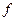 (
(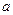 ));B(
));B(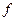 (-
(-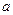 ),1),
),1),对任意
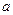 ∈(-1,1)恒有
∈(-1,1)恒有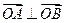 成立,试在
成立,试在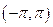 内求满足不等式
内求满足不等式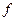 (sin
(sin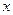 cos
cos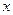 )+
)+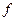 (cos2
(cos2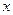 )>0的
)>0的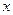 的取值范围.
的取值范围.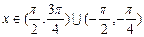 ,(
,(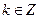 )
)向量与几何的综合运用

练习册系列答案
相关题目
题目内容
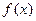 在定义域(-1,1)内可导,且
在定义域(-1,1)内可导,且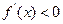 ,点A(1,
,点A(1,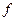 (
(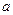 ));B(
));B(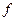 (-
(-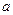 ),1),
),1),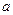 ∈(-1,1)恒有
∈(-1,1)恒有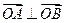 成立,试在
成立,试在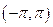 内求满足不等式
内求满足不等式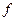 (sin
(sin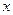 cos
cos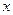 )+
)+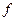 (cos2
(cos2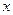 )>0的
)>0的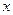 的取值范围.
的取值范围.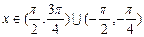 ,(
,(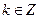 )
)