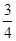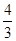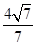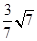题目内容
已知椭圆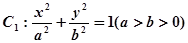 与双曲线
与双曲线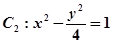 有公共的焦点,
有公共的焦点,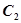 的一条渐近线与以
的一条渐近线与以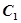 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若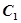 恰好将线段AB三等分,则
恰好将线段AB三等分,则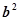 =
=
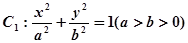 与双曲线
与双曲线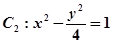 有公共的焦点,
有公共的焦点,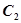 的一条渐近线与以
的一条渐近线与以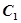 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若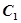 恰好将线段AB三等分,则
恰好将线段AB三等分,则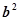 =
= 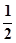
解:由题意,C2的焦点为(± 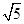 ,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
∴C1的半焦距c=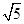 ,于是得a2-b2=5 ①
,于是得a2-b2=5 ①
设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得:x2="a2b2" b2+4a2 ②,
由对称性知直线y=2x被C1截得的弦长=2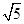 x,
x,
由题得:2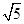 x="2a/" 3 ,所以x="a" /3
x="2a/" 3 ,所以x="a" /3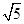 ③
③
由②③得a2=11b2 ④
由①④得a2=5.5,b2=0.5
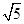 ,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a∴C1的半焦距c=
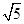 ,于是得a2-b2=5 ①
,于是得a2-b2=5 ①设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得:x2="a2b2" b2+4a2 ②,
由对称性知直线y=2x被C1截得的弦长=2
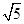 x,
x,由题得:2
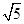 x="2a/" 3 ,所以x="a" /3
x="2a/" 3 ,所以x="a" /3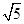 ③
③由②③得a2=11b2 ④
由①④得a2=5.5,b2=0.5

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
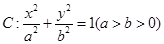 的焦点和上顶点分别为
的焦点和上顶点分别为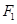 、
、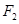 、
、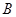 ,我们称
,我们称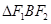 为椭圆
为椭圆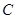 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断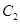 与
与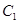 是否相似,如果相似则求出
是否相似,如果相似则求出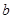 的椭圆为
的椭圆为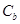 ,且直线
,且直线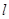 与椭圆为
与椭圆为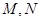 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,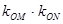 是否与
是否与
 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为

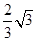

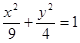 上一点
上一点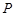 作圆
作圆 的两条切线,点
的两条切线,点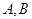 为切点.过
为切点.过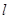 与
与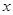 轴,
轴, 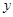 轴分别交于点
轴分别交于点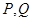 两点, 则
两点, 则 的面积的最小值为( )
的面积的最小值为( )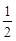
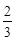
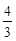
 ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程
的方程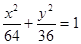 上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.
上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.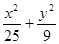 =1上任意一点,B为圆(x-1)2+y2=1上任意一点,则|AB|的最大值为________ 最小值为 ________
=1上任意一点,B为圆(x-1)2+y2=1上任意一点,则|AB|的最大值为________ 最小值为 ________  和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 点,若直线
点,若直线 恰与圆
恰与圆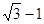



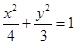 上的一点,
上的一点,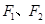 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若 的内切圆的半径为
的内切圆的半径为 ,则
,则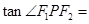 ( )
( )