题目内容
设 和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 经过椭圆的中心,且与椭圆相交于
经过椭圆的中心,且与椭圆相交于 点,若直线
点,若直线 恰与圆
恰与圆 相切,则该椭圆的离心率为( )
相切,则该椭圆的离心率为( )
 和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 经过椭圆的中心,且与椭圆相交于
经过椭圆的中心,且与椭圆相交于 点,若直线
点,若直线 恰与圆
恰与圆 相切,则该椭圆的离心率为( )
相切,则该椭圆的离心率为( )A.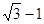 | B. | C. | D. |
A
由题意可知|MF2|=c,|F1F2|=2c,|MF1|= ,所以离心率为
,所以离心率为 .
.
 ,所以离心率为
,所以离心率为 .
.
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
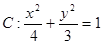 的右顶点是
的右顶点是 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形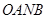 是矩形(
是矩形(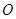 为原点),点
为原点),点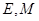 分别为线段
分别为线段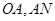 的中点.
的中点.
 与直线
与直线 的交点在椭圆
的交点在椭圆 上;
上;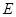 的直线交椭圆于
的直线交椭圆于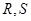 两点,
两点,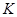 为
为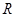 关于
关于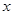 轴的对称点(
轴的对称点(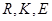 不共线),
不共线),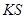 是否经过
是否经过 :
: 的离心率是
的离心率是 ,其左、右顶点分别为
,其左、右顶点分别为 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 .
. 为椭圆
为椭圆 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点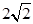 ,相应的焦点
,相应的焦点 的准线了l与x轴相交于A,|OF1|=2|F1A|.
的准线了l与x轴相交于A,|OF1|=2|F1A|. 轴上,且使MF2为
轴上,且使MF2为 的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;
的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点; 的“左特征点”的位置.
的“左特征点”的位置.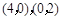 ,椭圆的方程是
,椭圆的方程是 或
或


 为椭圆
为椭圆 的左、右焦点,若
的左、右焦点,若 为椭圆上一点,且△
为椭圆上一点,且△ 的内切圆的周长等于
的内切圆的周长等于 ,则满足条件的点
,则满足条件的点 与双曲线
与双曲线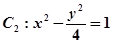 有公共的焦点,
有公共的焦点, 的一条渐近线与以
的一条渐近线与以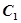 的长轴为直径的圆相交于A,B两点,若
的长轴为直径的圆相交于A,B两点,若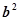 =
=  轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( )



 的左右焦点分别为
的左右焦点分别为 ,线段
,线段 被抛物线
被抛物线 的焦点分成5:3两段,则此椭圆的离心率为
的焦点分成5:3两段,则此椭圆的离心率为


