题目内容
已知双曲线 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为
 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为A. | B. | C.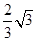 | D. |
C
解:因为双曲线 的焦点与椭圆
的焦点与椭圆 的焦点(2,0)(-2,0)重合
的焦点(2,0)(-2,0)重合
因此c=2,a2+1=4,所以a= ,因此离心率为e=
,因此离心率为e=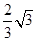 ,选C
,选C
 的焦点与椭圆
的焦点与椭圆 的焦点(2,0)(-2,0)重合
的焦点(2,0)(-2,0)重合因此c=2,a2+1=4,所以a=
 ,因此离心率为e=
,因此离心率为e=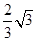 ,选C
,选C
练习册系列答案
相关题目
题目内容
 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为A. | B. | C.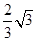 | D. |
 的焦点与椭圆
的焦点与椭圆 的焦点(2,0)(-2,0)重合
的焦点(2,0)(-2,0)重合 ,因此离心率为e=
,因此离心率为e=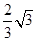 ,选C
,选C