题目内容
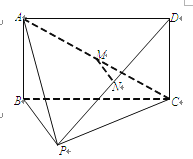
【题目】如图所示的多面体是由一个直平行六面体被平面![]() 所截后得到的,其中
所截后得到的,其中![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)底面![]() 中,根据余弦定理求
中,根据余弦定理求![]() ,三边满足勾股定理,所以
,三边满足勾股定理,所以![]() ,又根据原几何体是直平行六面体,所以
,又根据原几何体是直平行六面体,所以![]() ,也能证明
,也能证明![]() ,这样
,这样![]() 就垂直了平面内的两条相交直线,所以线面垂直;(Ⅱ)以点
就垂直了平面内的两条相交直线,所以线面垂直;(Ⅱ)以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立空间直角坐标系,求平面
轴建立空间直角坐标系,求平面![]() 的法向量
的法向量![]() ,根据公式
,根据公式![]() .
.
试题解析:(Ⅰ)证明:在![]() 中,∵
中,∵![]() ,
, ![]() .
.
由余弦定理![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
在直平行六面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
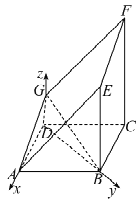
(Ⅱ)解:如图以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
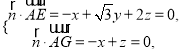 令
令![]() ,得
,得![]() ,
, ![]() ,
,
∴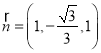 ,
,
设直线![]() 和平面
和平面![]() 的夹角为
的夹角为![]() ,
,
∴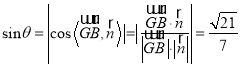 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目