题目内容
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点,求
两个不同的点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)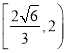 .
.
【解析】试题分析:(Ⅰ)直线与圆相交,根据弦长公式,求得![]() ,再根据椭圆过定点,建立方程,求得
,再根据椭圆过定点,建立方程,求得![]() ;(Ⅱ)设直线
;(Ⅱ)设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,根据弦长公式分别求
,根据弦长公式分别求![]() ,将
,将![]() 表示为
表示为![]() 的函数,求取值范围.
的函数,求取值范围.
试题解析:(Ⅰ)由已知可得:圆心到直线![]() 的距离为1,即
的距离为1,即![]() ,所以
,所以![]() ,
,
又椭圆![]() 经过点
经过点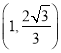 ,所以
,所以![]() ,得到
,得到![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程为
的方程为![]() ,
,
则![]() 的方程为
的方程为![]() .
.
由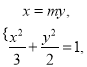 得
得 即
即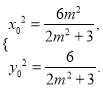
所以![]()
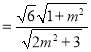 ,
,
由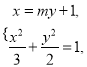 ,得
,得![]() ,
,
所以![]() ,
, ![]() ,
,
![]()
![]()
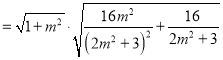
![]() ,
,
所以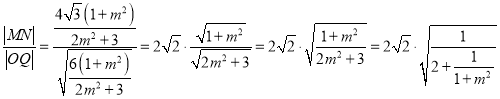 ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,即
,即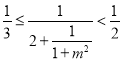 ,
,
所以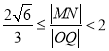 ,即
,即![]() 的取值范围为
的取值范围为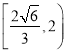 .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】【2015高考山东文数】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.