题目内容
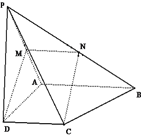
【题目】如图，在四棱锥P－ABCD中，四边形ABCD为矩形，AB⊥BP，M为AC的中点，N为PD上一点.
（1）若MN∥平面ABP，求证：N为PD的中点；
（2）若平面ABP⊥平面APC，求证：PC⊥平面ABP.
【答案】（1）见解析（2）见解析
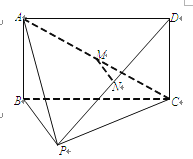
【解析】试题分析：（1）由线面平行性质定理得MN∥BP，再根据三角形中位线性质得N为PD的中点.（2）过点B作BE⊥AP，则根据面面垂直性质定理得BE⊥平面APC，即BE⊥PC.又易得AB⊥平面BPC，即AB⊥PC，最后根据线面垂直判定定理得PC⊥平面ABP
试题解析：（1）连接BD，由四边形
为矩形得：M为
和
的中点，∵MN∥平面ABP，MN平面BPD，平面BPD
平面ABP＝BP，∴MN∥BP，∵M为AC的中点，∴N为PD的中点.
（2）在△ABP中，过点B作BE⊥AP于E，∵平面ABP⊥平面APC，平面ABP∩平面APC＝AP，BE平面ABP，BE⊥AP
∴BE⊥平面APC， 又PC平面APC，∴BE⊥PC.∵ABCD为矩形，∴ AB⊥BC，又AB⊥BP，BC∩BP＝B，BC，BP 平面BPC，∴AB⊥平面BPC， ∴AB⊥PC，又BE⊥PC， AB平面ABP，BE平面ABP，AB∩BE＝B， ∴PC⊥平面ABP
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知数列{xn}满足x1=1，x2=λ，并且 
=λ 
（λ为非零常数，n=2，3，4，…）． （Ⅰ）若x1 ， x3 ， x5成等比数列，求λ的值；
（Ⅱ）设0＜λ＜1，常数k∈N* ， 证明 
．
