题目内容
【题目】若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.
(1)点M(x,y)横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点M(x,y)落在上述区域的概率?
(2)试求方程x2+2px﹣q2+1=0有两个实数根的概率.
【答案】
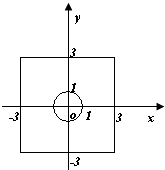
(1)解:根据题意,点(p,q),在|p|≤3,|q|≤3中,即在如图的正方形区域,
其中p、q都是整数的点有6×6=36个,
点M(x,y)横、纵坐标分别由掷骰子确定,即x、y都是整数,且1≤x≤3,1≤y≤3,
点M(x,y)落在上述区域有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),有9个点,
所以点M(x,y)落在上述区域的概率P1= ![]()
(2)解:|p|≤3,|q|≤3表示如图的正方形区域,易得其面积为36;
若方程x2+2px﹣q2+1=0有两个实数根,则有△=(2p)2﹣4(﹣q2+1)≥0,
解可得p2+q2≥1,为如图所示正方形中圆以外的区域,其面积为36﹣π,
即方程x2+2px﹣q2+1=0有两个实数根的概率,P2= ![]() .
.
【解析】(1)是古典概型,首先分析可得|p|≤3,|q|≤3整点的个数,进而分析可得点M的纵横坐标的范围,可得M的个数,由古典概型公式,计算可得答案;(2)是几何概型,首先可得|p|≤3,|q|≤3表示正方形区域,易得其面积,进而根据方程x2+2px﹣q2+1=0有两个实数根,则有△=(2p)2﹣4(﹣q2+1)≥0,变形可得p2+q2≥1,分析可得其表示的区域即面积,由几何概型公式,计算可得答案.
【考点精析】根据题目的已知条件,利用几何概型的相关知识可以得到问题的答案,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).
).
(Ⅰ)把曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(Ⅱ)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.