题目内容
【题目】如图，扇形的半径为r cm，周长为20cm，问扇形的圆心角α等于多少弧度时，这个扇形的面积最大，并求出扇形面积的最大值．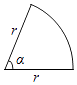 
【答案】解：设扇形的半径为r，弧长为l，则：l+2r=20，即l=20﹣2r（0＜r＜10）． 扇形的面积S= 
lr，将上式代入，得：S= （20﹣2r）r=﹣r2+10r=﹣（r﹣5）2+25，
所以：当且仅当r=5时，S有最大值25，
此时：l=20﹣2×5=10，α= 
=2rad．
所以：当α=2rad时，扇形的面积取最大值，最大值为25cm2
【解析】设扇形的半径为r，弧长为l，利用周长关系，表示出扇形的面积，利用二次函数求出面积的最大值，以及圆心角的大小．
【考点精析】本题主要考查了扇形面积公式的相关知识点，需要掌握若扇形的圆心角为
，半径为
，弧长为
，周长为
，面积为
，则
，
，
才能正确解答此题．
练习册系列答案
相关题目
【题目】已知数列{xn}满足x1=1，x2=λ，并且 
=λ 
（λ为非零常数，n=2，3，4，…）． （Ⅰ）若x1 ， x3 ， x5成等比数列，求λ的值；
（Ⅱ）设0＜λ＜1，常数k∈N* ， 证明 
．
【题目】【2015高考山东文数】某中学调查了某班全部
名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
（1）从该班随机选
名同学，求该同学至少参加上述一个社团的概率；
（2）在既参加书法社团又参加演讲社团的
名同学中，有5名男同学
名女同学
现从这
名男同学和名女同学中各随机选
人，求
被选中且
未被选中的概率.
