题目内容
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点.
两个不同的点.
(1)试探究![]() 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
(2)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ; (Ⅱ)(1)
; (Ⅱ)(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)直线与圆相交,根据弦长公式,求得![]() ,再根据椭圆过定点,建立方程,求得
,再根据椭圆过定点,建立方程,求得![]() ;(Ⅱ)(1)设直线
;(Ⅱ)(1)设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,根据弦长公式分别求
,根据弦长公式分别求![]() ,将
,将![]() 表示为
表示为![]() 的式子,求定值;(2)将面积表示为
的式子,求定值;(2)将面积表示为![]() 的函数,再通过换元,求函数的最值.
的函数,再通过换元,求函数的最值.
试题解析:(Ⅰ)由已知可得:圆心到直线![]() 的距离为1,即
的距离为1,即![]() ,所以
,所以![]() ,
,
又椭圆![]() 经过点
经过点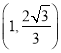 ,所以
,所以![]() ,得到
,得到![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(1)设![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程为
的方程为![]() ,
,
则![]() 的方程为
的方程为![]() .
.
由 得
得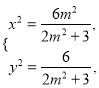 即
即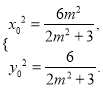
所以![]()
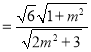 ,
,
由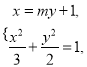 ,得
,得![]() ,
,
所以![]() ,
, ![]() ,
,
![]()
![]()
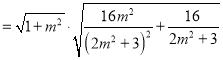
![]() ,
,
所以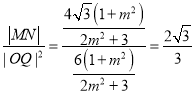 .
.
(2)∵![]() ,∴
,∴![]() 的面积
的面积![]() 的面积,∴
的面积,∴![]() ,
,
∵![]() 到直线
到直线![]() :
: ![]() 的距离
的距离![]() ,
,
∴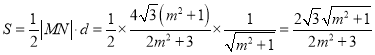 ,令
,令![]() ,则
,则![]() (
(![]() ),
),
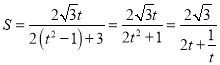 ,
,
令![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上为增函数,
上为增函数, ![]() ,
, ![]() .
.

练习册系列答案
相关题目
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.