题目内容
15.在△ABC中,AC=BC=$\sqrt{5}$,AB=2,点O为AB的中点,点E,F分别在BC、CA上,且EF=1,点M是线段EF的中点,若$\overrightarrow{OE}$•$\overrightarrow{OF}$≤$\frac{25}{16}$,则|$\overrightarrow{OM}$|的最大值为$\frac{\sqrt{65}}{4}$.分析 以O为坐标原点,AB所在直线为x轴,建立直角坐标系,直线AC:y=2x+2,BC:y=-2x+2,设E(m,2m+2),F(n,2-2n),中点M($\frac{1}{2}$(m+n),2+m-n),由EF=1,可得(m-n)2+(2m+2n)2=1,若$\overrightarrow{OE}$•$\overrightarrow{OF}$≤$\frac{25}{16}$,则mn+(2m+2)(2-2n)≤$\frac{25}{16}$,而|$\overrightarrow{OM}$|=$\sqrt{\frac{1}{4}(m+n)^{2}+(2+m-n)^{2}}$=$\sqrt{\frac{15}{16}(m-n)^{2}+4(m-n)+\frac{65}{16}}$,由-1≤m-n≤0,由对称轴-$\frac{32}{15}$<-1,利用二次函数的单调性即可得出.
解答 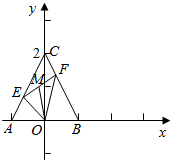 解:以O为坐标原点,AB所在直线为x轴,建立直角坐标系,
解:以O为坐标原点,AB所在直线为x轴,建立直角坐标系,
A(-1,0),B(1,0),C(0,2),
直线AC:y=2x+2,BC:y=-2x+2,
设E(m,2m+2),F(n,2-2n),
中点M($\frac{1}{2}$(m+n),2+m-n),
由EF=1,可得(m-n)2+(2m+2n)2=1,
若$\overrightarrow{OE}$•$\overrightarrow{OF}$≤$\frac{25}{16}$,则mn+(2m+2)(2-2n)≤$\frac{25}{16}$,
而|$\overrightarrow{OM}$|=$\sqrt{\frac{1}{4}(m+n)^{2}+(2+m-n)^{2}}$
=$\sqrt{\frac{1}{16}(1-(m-n)^{2})+(2+m-n)^{2}}$
=$\sqrt{\frac{15}{16}(m-n)^{2}+4(m-n)+\frac{65}{16}}$,
由-1≤m-n≤0,
由对称轴-$\frac{32}{15}$<-1,即有m-n=0时,
取得最大值,且为$\frac{\sqrt{65}}{4}$.
故答案为:$\frac{\sqrt{65}}{4}$.
点评 本题考查了向量的坐标运算、中点坐标公式、数量积运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{3}{4}$πR2 | B. | $\frac{9}{2}$πR2 | C. | $\frac{9}{4}$πR2 | D. | $\frac{9}{8}$πR2 |