题目内容
20.已知椭圆C的两个焦点分别为F1($-\sqrt{10}$,0),F2($\sqrt{10}$,0),且椭圆C过点P(3,2).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求证:直线PA,PB与y轴围成一个等腰三角形.
分析 (Ⅰ)由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,利用椭圆定义求得a,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)求出${k}_{OP}=\frac{2}{3}$,设与直线OP平行的直线方程为y=$\frac{2}{3}x+m$,联立直线和椭圆方程,由根与系数关系求出A,B两点横坐标的和与积,代入两直线的斜率和得答案.
解答 (Ⅰ)解:由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
∵椭圆C的两个焦点分别为F1($-\sqrt{10}$,0),F2($\sqrt{10}$,0),且椭圆C过点P(3,2),
由椭圆定义可得2a=$\sqrt{(3+\sqrt{10})^{2}+{2}^{2}}+\sqrt{(3-\sqrt{10})^{2}+{2}^{2}}$=$2\sqrt{18}$,即a=$\sqrt{18}$,
∴b2=a2-c2=8,则椭圆C的标准方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{8}=1$;
(Ⅱ)证明:∵${k}_{OP}=\frac{2}{3}$,
∴设与直线OP平行的直线方程为y=$\frac{2}{3}x+m$,
联立$\left\{\begin{array}{l}{y=\frac{2}{3}x+m}\\{\frac{{x}^{2}}{18}+\frac{{y}^{2}}{8}=1}\end{array}\right.$,得8x2+12mx+9m2-72=0.
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{3}{2}m$,${x}_{1}{x}_{2}=\frac{9{m}^{2}-72}{8}$.
设直线PA,PB的斜率分别为k1,k2,
∵${k}_{1}+{k}_{2}=\frac{2-{y}_{1}}{3-{x}_{1}}+\frac{2-{y}_{2}}{3-{x}_{2}}$=$\frac{(2-\frac{2}{3}{x}_{1}-m)(3-{x}_{2})+(2-\frac{2}{3}{x}_{2}-m)(3-{x}_{1})}{(3-{x}_{1})(3-{x}_{2})}$
=$\frac{(m-4)({x}_{1}+{x}_{2})+\frac{4}{3}{x}_{1}{x}_{2}+12-6m}{(3-{x}_{1})(3-{x}_{2})}$=$\frac{(m-4)(-\frac{3}{2}m)+\frac{4}{3}•\frac{9{m}^{2}-72}{8}+12-6m}{(3-{x}_{1})(3-{x}_{2})}=0$.
∴直线PA,PB与y轴围成一个等腰三角形.
点评 本题考查椭圆方程的求法,考查直线MA,MB与x轴围成一个等腰三角形的证明,训练了根与系数的关系的应用,考查计算能力,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
| A. | y=-4x+3 | B. | y=-4x-3 | C. | y=4x+3 | D. | y=4x-3 |
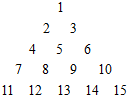 把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.