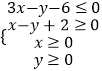Question

【题目】已知命题p：x1 ， x2是方程x2﹣mx﹣1=0的两个实根，且不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立；命题q：不等式x2+2x+a＜0有解，若命题p∨q为真，p∧q为假，求a的取值范围．

Answer 1

【答案】解：命题p：x1 ， x2是方程x2﹣mx﹣1=0的两个实根，∴△=m2+4≥0．x1+x2=m，x1x2=﹣1．
∴|x1﹣x2|= = ．
∵不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立，∴a2+4a﹣3≤2，解得﹣5≤a≤1；
命题q：不等式x2+2x+a＜0有解，∴△=4﹣4a＞0，解得a＜1．
∵命题p∨q为真，p∧q为假，
∴p与q必然一真一假，
∴ ，或 ，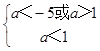
解得a=1，或a＜﹣5．
∴a的取值范围是a=1或a＜﹣5
【解析】命题p：x1 ， x2是方程x2﹣mx﹣1=0的两个实根，可得△≥0．利用根与系数的关系|x1﹣x2|= = ．即可得出最小值．不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立，解得a范围；命题q：不等式x2+2x+a＜0有解，可得△＞0，解得a范围．由于命题p∨q为真，p∧q为假，可得p与q必然一真一假，即可得出．
【考点精析】本题主要考查了复合命题的真假的相关知识点，需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真才能正确解答此题．