题目内容
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面积为10
,△ABC的面积为10 ![]() ,求BC边上的中线长.
,求BC边上的中线长. 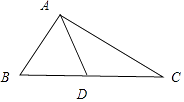
【答案】
(1)解:∵cos2B﹣5cos(A+C)=2.
∴2cos2B+5cosB﹣3=0,解得:cosB= ![]() 或﹣3(舍去),又B∈(0,π),
或﹣3(舍去),又B∈(0,π),
∴B= ![]()
(2)解:∵cosA= ![]() ,∴可得:sinA=
,∴可得:sinA= ![]() ,
,
∴sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
设b=7x,c=5x,则在△ABC中,由余弦定理得BC2=AB2+AC2﹣2ABACcosA,
∴BC= ![]() =8x,
=8x,
∵△ABC的面积为10 ![]() =
= ![]() ABBCsinB=
ABBCsinB= ![]() ×5x×8x×
×5x×8x× ![]() ,解得:x=1,
,解得:x=1,
∴AB=5,BC=8,AC=7,BD=4,
∴在△ABD中,由余弦定理得AD2=AB2+BD2﹣2ABBDcosB=25+16﹣2×5×4× ![]() =21,
=21,
∴解得:AD= ![]() .
.
【解析】(1)利用三角函数恒等变换的应用化简已知等式可得2cos2B+5cosB﹣3=0,进而解得cosB,结合B的范围即可得解B的值;(2)先根据两角和差的正弦公式求出sinC,再根据正弦定理得到b,c的关系,再利用余弦定理可求BC的值,再由三角形面积公式可求AB,BD的值,利用余弦定理即可得解AD的值.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.

练习册系列答案
相关题目
